ジュニア問題/Bガラスのコップ
ガラスのコップ
テーブルの上に、何も入っていないコップが5個あります。1個は上下が逆さに置かれています。あなたは「3個のコップの上下をひっくり返す」操作ができます。
（必ず3個を同時にひっくり返す必要があります）
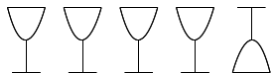
すべてのコップを上向きにするために、「3個のコップの上下をひっくり返す」操作は最低何回必要ですか。
- 解説を見る
- 正解は「3回」
3個をひっくり返せるということは、次のどちらかの操作ができる- 「上上下を選んで下下上にする」のように、2個の上向きのコップと1個の下向きのコップを選んで、下向きのコップを1個増やせる
- 「下下下を選んで上上上にする」のように、下向きのコップ3個をすべて上向きにできる
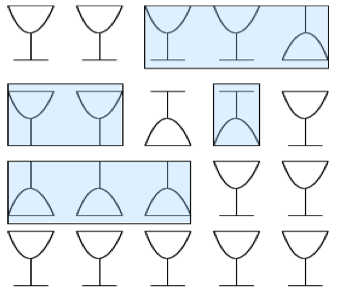
- 解説
この問題は、アルゴリズムに従い、「システム」や「変数」の状態を追跡する問題です。この問題の状態は「上向きのコップの個数」（この値がわかれば「下向きのコップの個数」も決定できます）です。
- 正解は「3回」
注があるものを除き, このサイトの内容物は
