2023-橋をかける仕事-解説
- 考案国:ニュージーランド
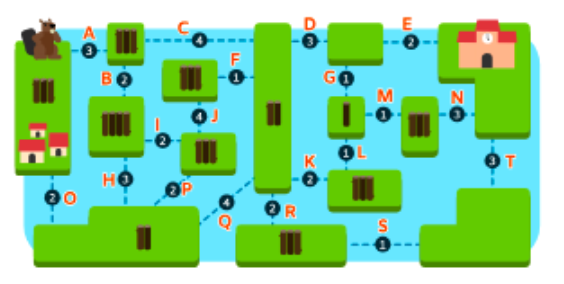
- 正解
- 説明
- 各ステップで拾った丸太の累積数と使用した丸太の累積数を記録することで,正しい経路が実行可能であること(各ステップで拾った丸太数 ≥ 使用した丸太数)を示すことができます:(3,2)(5,4)(8,4)(8,8)(10,10)(13,11)(14,12)(14,14)。
- 丸太の使用数が14本以下のケースで,村と学校を結ぶ全ての経路を見つけ,上記の正しい回答だけが実現可能であることを示すことで,これが最小であることを証明することができます。まず,すべての経路が中央の大きな島を通る必要があるため,問題を二つの部分に分けることができます。次に,村から中央までの経路には少なくとも6本の丸太が必要であり,中央から学校までの経路には少なくとも5本が必要です(これを下界と呼びます)。
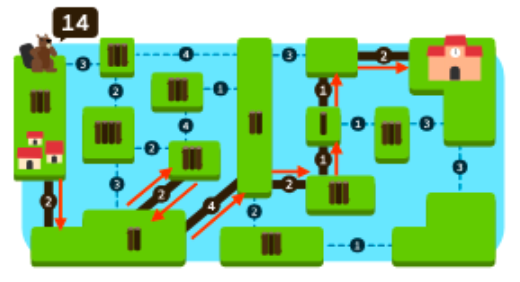
まず、右側の下限(5本)を考慮して左側の部分を解決します。右側の下限は5本なので,左側は9本以下の丸太を使用する可能な経路を探すことにします。左側では,以下の経路が中央まで繋がり,9本以下の丸太を使用します(拾った丸太,使用した丸太)。
{A,C}=(6,7),{A,B,C}=(10,9),{O,Q}=(5,6),{O,H,Q}=(9,9),{O,P,Q}=(8,8),{O,P,J,F}=(11,9)
「拾った丸太 < 使用した丸太」となった実現不可能な解決策を除去すると,次のようになります。
{A,B,C}=(10,9),{O,H,Q}=(9,9),{O,P,Q}=(8,8),{O,P,J,F}=(11,9)
次に,左側で8本の使用丸太を下限として右側を解決するため,6本以下の丸太を使用するすべての経路を探します。
{D,E}=(2,5),{D,G,E}=(3,6),{K,L,G,E}=(6,6),{R,S,T}=(5,6)
左側と右側の解決策を組み合わせて,合計で14本以下の丸太を使用する可能性のある組み合わせを探すと,{O,P,Q}=(8,8)+{K,L,G,E}=(6,6) → (14,14) となります。
- 実際のコンピュータでは
- この問題での陸地と橋は,グラフ理論でのノードとエッジとして表現することができます。各陸地で拾われたり,橋を建設するために使われる丸太の数は,それぞれのノードとエッジに割り当てることができます。
- この問題を一般的に解決するには,資源制約付きの経路探索アルゴリズムを使用することができます。すべての有効な経路を徹底的に検索する力任せの方法も有効ですが,計算時間はグラフのサイズが大きくなるにつれて指数関数的に増加します。
- 別の方法として,この問題の解法が示すように,分割統治法として考えることもできます。このアプローチは,パス整合性や分岐限定法などの制約最適化の技術を使用します。これらの技術は,実世界の資源配分問題,パズル(例えば数独のような),およびゲームプレイ人工知能などの基礎となっています。
 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は