2023-ビバ子の買い物-解説
- 考案国:ベルギー
- 正解
- 39分
- 説明
- 正解は39分です。最短時間でのルートは以下の通りです:
- エマの家 → 学校 → 薬局 → 学校 → 教会 → パン屋 → 鍛冶屋 → パン屋 → 市場 → エマの家
- これには6 + 3 + 3 + 4 + 4 + 3 + 3 + 6 + 4 = 36分が必要で,買い物に3分 = 合計39分です。彼女はこの道を逆方向にたどっても同じ時間がかかります。
- より短いルートがないことを確認するために,地図の簡略版を使用します。
- 下の図をご覧ください:

丸印(ノードや頂点と呼びます)は村の異なる場所を表し,線(エッジや辺と呼びます)はそれらの間の道を表します。地図にあるように,各エッジの隣の数字は,その道を歩くのにかかる時間を示しています。 - 灰色のエッジは無視できます(下図参照)。中間ノードを経由するより速いルートがあるからです。
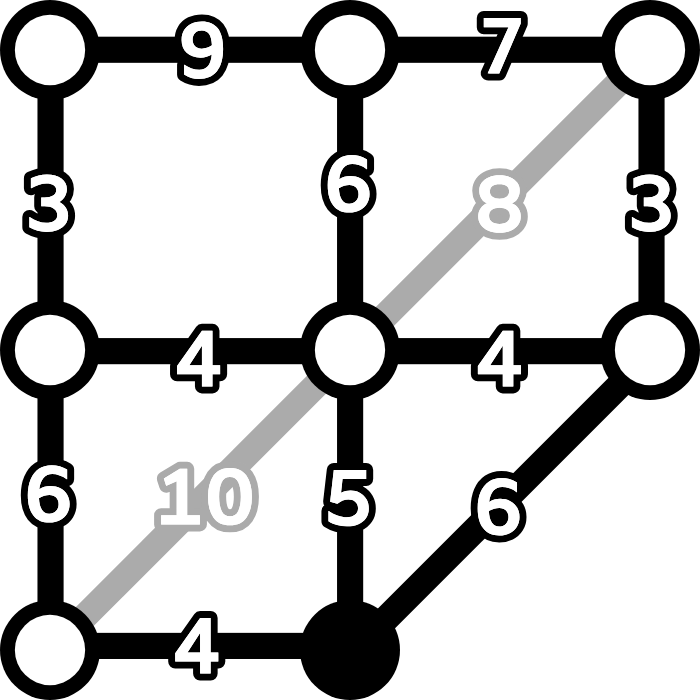
- 「公園」のノードも無視できます。公園でのタスクがなく,公園を通るすべてのルートにはより速い代替ルートがあるからです。
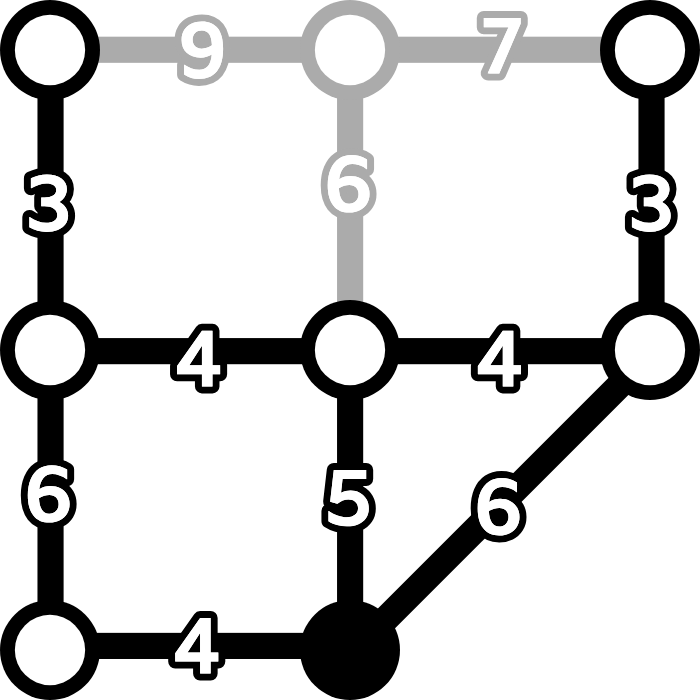
- 残った図の上部にある2つのノード(鍛冶屋と薬局)はビバ子が訪れる必要があります。これは常にその直下のノードを通って行われ,どちらの場合もそこまで3分,戻るのに3分かかります。
- これらのノードを取り除き,最終結果に12分を追加することを覚えておきます。
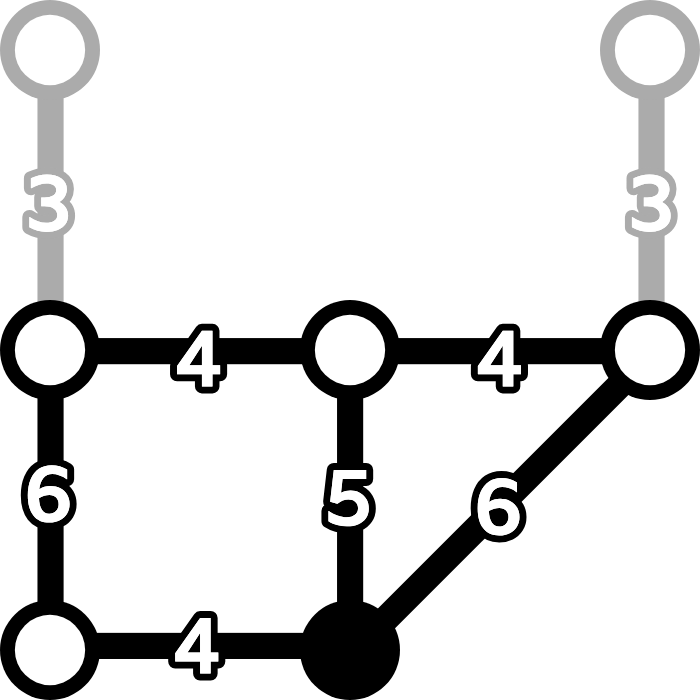
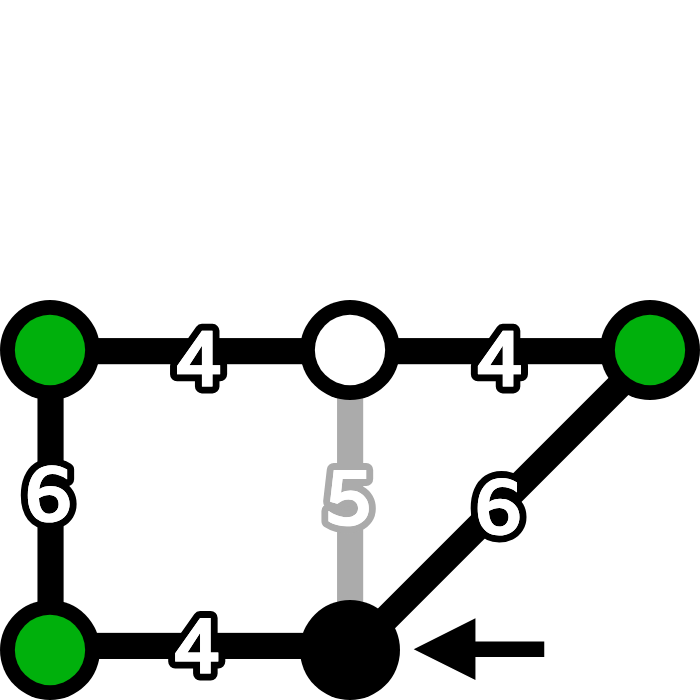
- 最終的に右図のようになります。矢印がある右下のノードで始めて終わり,3つの色付きノードをすべて訪れる必要があります。最短のルートは,灰色に塗られたエッジを除いて5つのノードを通ります。
- このルートには4 + 6 + 4 + 4 + 6 = 24分かかります。前のステップからの12分と各訪問地でのタスクを完了するのに3分を加えると,合計時間は39分になります。
- 下の図をご覧ください:
- 正解は39分です。最短時間でのルートは以下の通りです:
- 実際のコンピュータでは
- 最短ルートを見つけるために使用した簡略化された図は,グラフと呼ばれます。コンピュータサイエンスの多くの問題は,このようにグラフを作って,解析することで解かれます。この問題では,グラフ内の特定のノードを通る最短経路を見つけようとしています。
- コンピュータは「最短経路」問題をもっと多くのノードとエッジを持つ場合に使用されます。例えば,交通や流通の問題で,ゴミ収集車,郵便配達員,または牛乳配達車が巡回する最短経路を計算するために使用されます。
- 問題をモデル化するためにグラフを使用することは,抽象化と呼ばれます。私たちは様々な場所の名前やそれらを結ぶ道の形状については(ここでは重要ではないので)考えないようにして(捨象,といいます),どの場所がどの場所とつながっているか,とそれらの移動にかかる時間に集中して考えます。この抽象化が問題の解決に役立ちます。
- 地図自体も村を抽象化したものです。このように,抽象化という概念を知ったり,使ったりすることも,計算論的思考 (Computational Thinking) の一部です。
 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は