2023-ウォーキング・ホリデー-解説
- 考案国：アメリカ
- 正解
- 6
- 説明
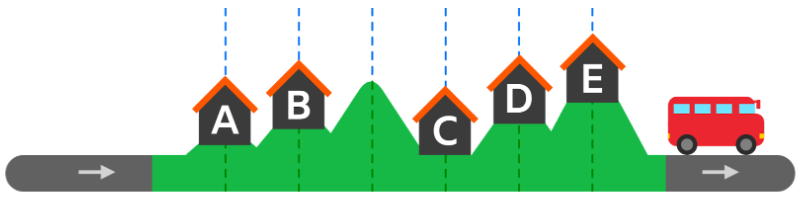
- 問題を分解して考えることで考えてみましょう。まず，ビバ子はBとCに滞在しなければならないことに気づきます。これらの2つの場所の距離は２であり，ビバ子が1日で歩ける最大の距離だからです。これにより，この前後の二つのセクションを2つの小さな問題として考えることができます。
- まず，スタートからBまで行く方法について考えます。方法は2つあります（ルート1とルート2に示されている方法）。したがって，Cへの可能なルートも2つということになります。
- 次に，Cから終点までに行く方法について考えます。これについては，次の3つの可能性があります。
- C → D → E → End
- C → E → End
- C → D → End
- このようにして，前半で２通り，後半で３通り，合計で2 x 3 = 6つの可能なルートがあることがわかります。
- 実際のコンピュータでは
- 説明にあるように，この問題は2つの小さな問題に分解して解決することができます。同様の大きな問題では，動的計画法での解決策が採用されます。アルゴリズムが問題を非常に小さな部分問題に分解し，小さな問題の解決策を使用して大きな解決策を作り出す戦略です。
- タート，A，B，C，D，E，エンドという場所に番号を付けると，各場所に到達する方法が何通りあるかの表を作ることができます。
場所 到達方法 スタート 1 A 1 (スタートから到達できる) B 1 + 1 = 2 (スタートから直接来るかAを経由する) C 2 (Bから来る必要がある) D 2 (Cから来る必要がある) E 2 + 2 = 4 (BかCから来る) End 2 + 4 = 6 (DかEから来る) - 説明でみたように，一つ一つ課題を分割して上記の表を埋めていくことを動的計画法と呼びます。これは，人間が解決するのに時間がかかるような大きな問題に対しても解決策を見つけることができる，コンピュータが得意なアルゴリズムです。
- 説明にあるように，この問題は2つの小さな問題に分解して解決することができます。同様の大きな問題では，動的計画法での解決策が採用されます。アルゴリズムが問題を非常に小さな部分問題に分解し，小さな問題の解決策を使用して大きな解決策を作り出す戦略です。
注があるものを除き, このサイトの内容物は
