2023-ある日の動物園-解説
- 考案国：オーストリア
- 正解
- 5
- 説明
- この問題を解決する方法の一つは，重ならないショーの可能な組み合わせをすべて試すことです。重ならないショーの組み合わせは，実際に見ることが可能なスケジュールです。その後，見ることができるショーが最も多いスケジュール（最適なスケジュール）を確認します。この方法は，全探索やしらみつぶし探索などと呼ばれます。
- 解決すべき問題によっては，全探索では確認しないとならない組み合わせが多くなり，現実的な時間で解が得られないことがあります。
- 問題をよく観察することで，問題を簡単にする緒（いとぐち）を見出すことができます。もし２つのショーの時間が重なっている場合，最適なスケジュールに含まれるのはどちらか1つのショーだけです。これら２つのショーのうち，1つのショーの時間がもう１つのショーの時間に完全に他に含まれている場合は，短い時間のショーを選ぶべきです。
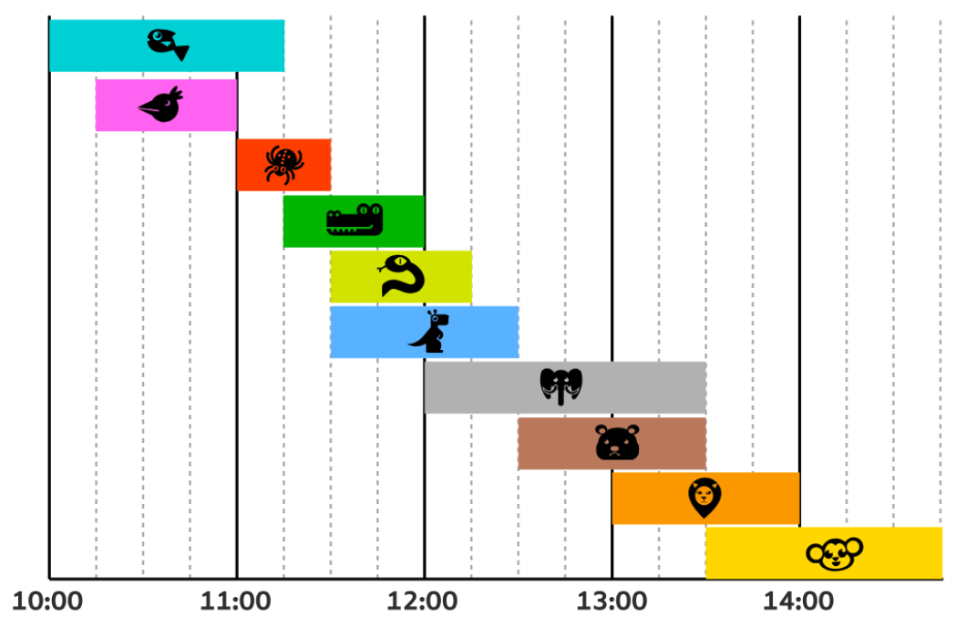
- 例えば，鳥のショー
の時間は魚のショー 
の時間に含まれています。
魚のショー を選ぶのなら， 鳥のショー を選んだ方が，これら２つ以外のショーと重なる可能性が小さくなります。
よって，鳥のショー は考察から外すことができます。 - 同じ理由で，次のことが言えます。
- ヘビのショー
はカンガルーのショー 
の間に行われるので， カンガルーのショー を考察から外すことができます。 - クマのショー
は象のショー 
の間に行われるので， 象のショー を考察から外すことができます。
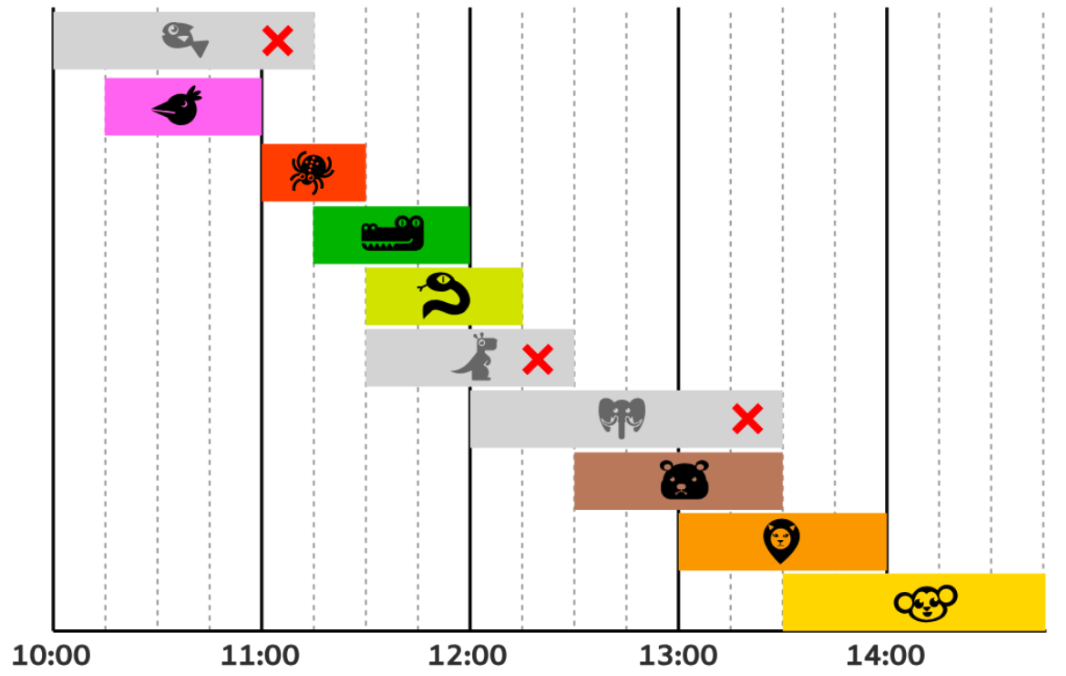
- ヘビのショー
- これら３つのショーを取り除くと，残ったショーは次の図のようになります:
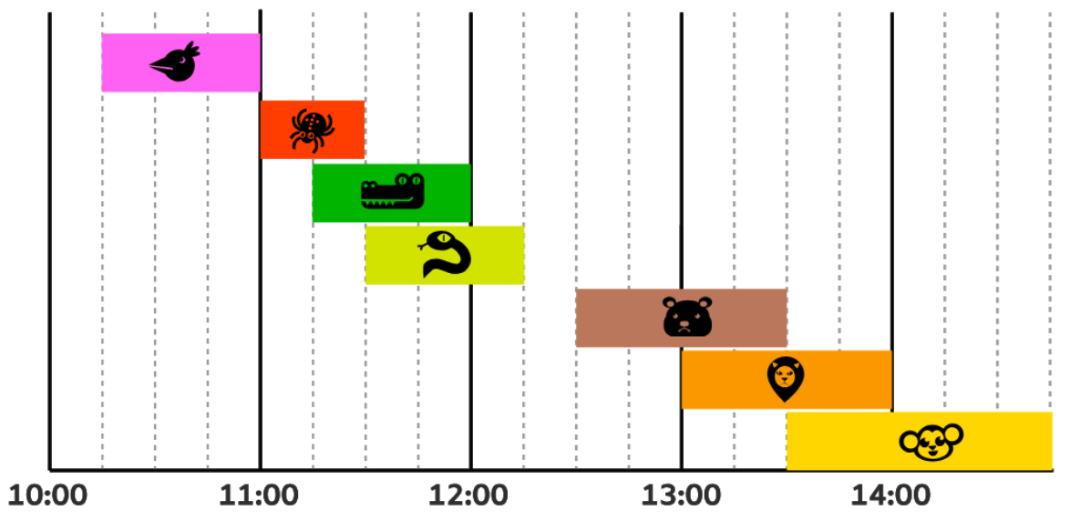
- これらのショーを時間が重ならならない３つのグループに分けて， A, B, C を名前をつけることにします。すると，それぞれのグループで最適なスケジュールを求めることで，1日全体の最適なスケジュールを求めることができます。
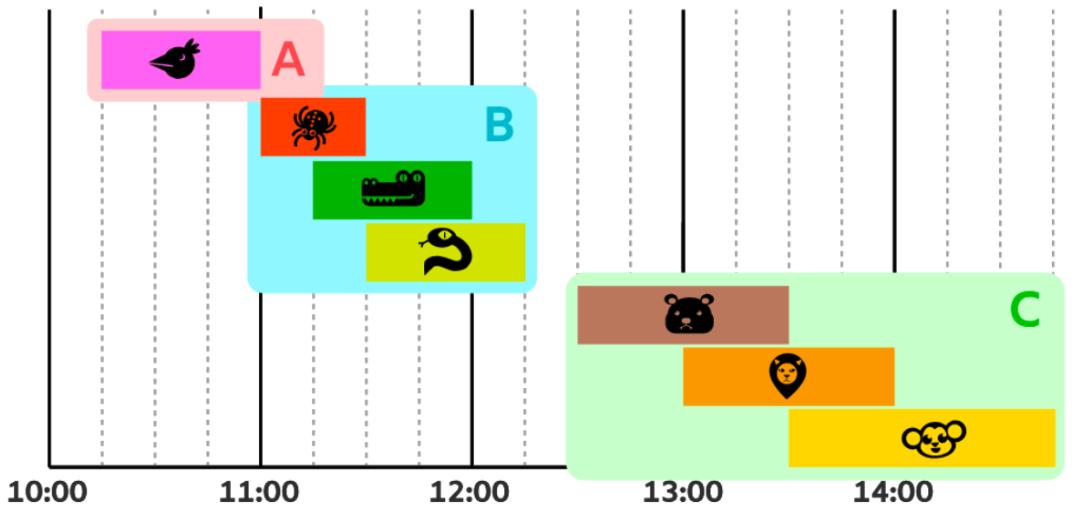
- グループ A には，鳥のショー だけが含まれています。そこで最適なスケジュールに鳥のショー を入れます。
- グループ B には3つのショーが含まれています。
グループ B を全探索すると実現可能なスケジュールは２つです。
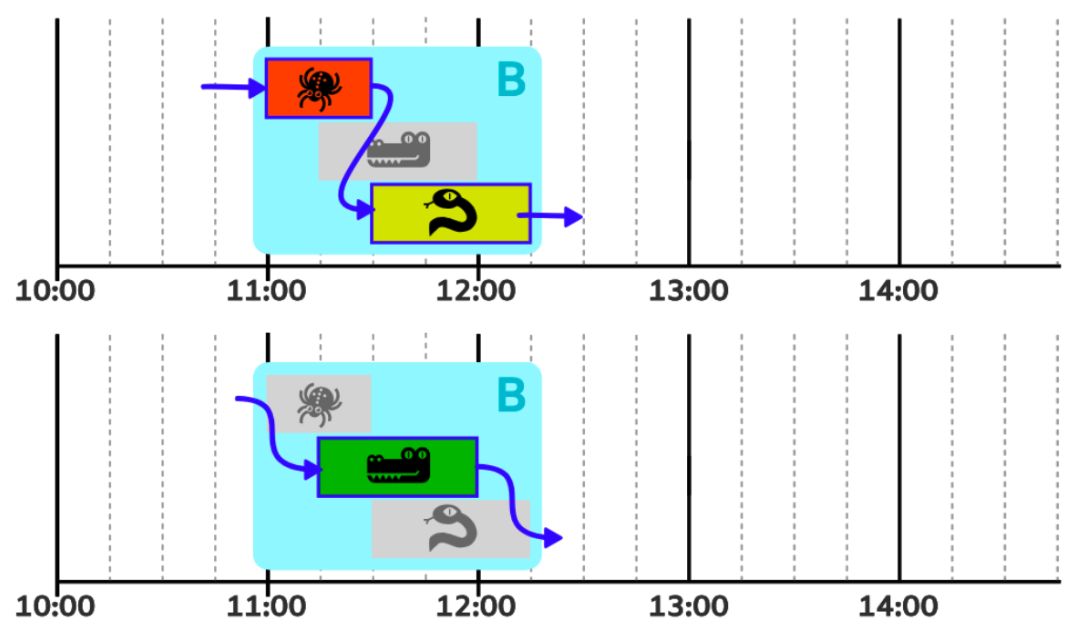
グループ B から最適なスケジュールに入れるのはクモのショー
とヘビのショー です。 - グループ C にも3つのショーが含まれています。同じように全探索することで，グループ C からはアザラシのショーtとコアラのショーを最適なスケジュールに入ることが分かります。
- グループ A には，鳥のショー
- これらをまとめると1日全体の最適なスケジュールは次の図のようになります:
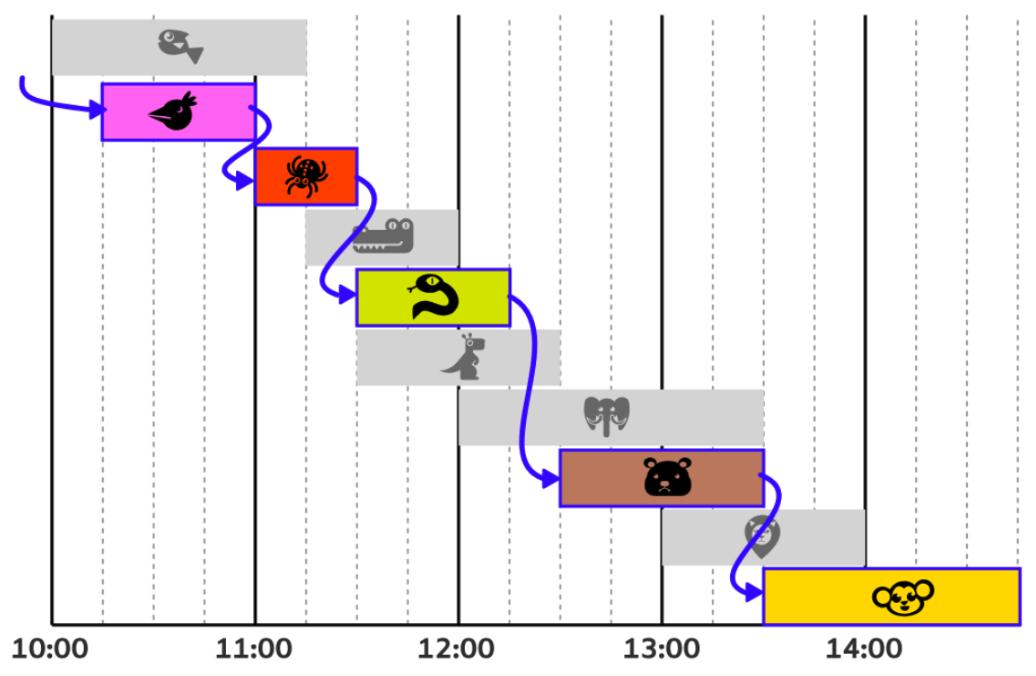
このスケジュールには5つのショーが含まれているので，正解は 5 です。
- 実際のコンピュータでは
- 情報学において，問題を解決するアルゴリズムを設計する際，最も簡単に思いつくアルゴリズムは，全探索・しらみつぶし探索です。この探索法は，概念が単純でかつ正しい答えを保証します。しかし，全探索は手作業やコンピュータで行うにも時間がかかりすぎることです。もっと高速に問題を解決するためのより効率的なアルゴリズムを見つける必要があります。
- アルゴリズムをより効率化するには，問題を良く観察して，問題を解決するのに必要な項目だけを抜き出すことが重要となります。このことを，簡略化や抽象化と呼ぶことにします。解の値を最大化または最小化する問題は最適化問題と呼ばれます。最適化問題を簡略化する際に，最適な解を得るための情報は残す必要があります。この問題では，魚のショー、コアラのショー、象のショーなどを無視できました。なぜなら，これらのショーを含むスケジュールは，別のショーを選ぶことで，見られるショーの数が同じかより多いスケジュールを構成できるからです。
- アルゴリズムをより効率化するもう一つの戦略は，問題を独立した部分，つまり部分問題に分解することです。コンピュータは異なる入力に対して同じ処理を繰り返し行うのが得意なので，独立した部分問題に適用できるアルゴリズムを見つけることは実現的な戦略です。
- 問題の解法の説明でも，問題を独立して解決できるより小さな部分に分解しています。
- 一般的に，特定の期間における複数のショーから見ることができる最大数を選ぶ処理は，活動選択問題ｙａインターバルスケジューリング問題と呼ばれます。大規模な工場でのプロセス管理や単一のコンピュータでの多くのプログラムの実行において，数千または数百万の活動を含む活動選択問題が生じるかもしれません。情報学では，総当たり探索を使わずにこれらの問題を解決するさらに高度なアルゴリズムが開発されています。
- この問題では，最大の解を見つけるための戦略を開発する必要があります。ショーの開催時間の重複を分析し，最適な解に含めるべきショーと考慮しなくても良いショーの見分かることで実現できます。
注があるものを除き, このサイトの内容物は
