2017-壁を壊せ-解説
- 考案国:スロバキア
- 正解
- 説明
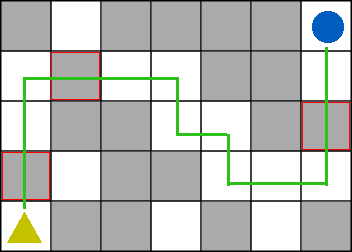
- 左下の角(かど)から右上の角まで移動できるようにするのに壊す壁(かべ)の最小値は 3 です。
下の図で赤で囲まれた3つの壁を壊せば、左下のかどから右上の角まで移動できるようになります。
緑の線は、左下の角から右上の角まで移動する道順です。
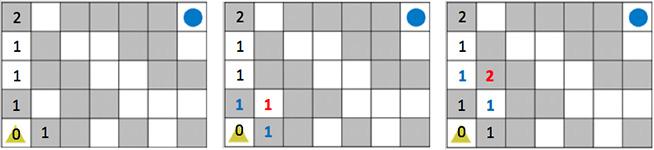
この問題を必ず解ける手順の一つは、左下の角から順に「その場所に左下の角から到達するのに壊さないとならない壁の最小値」を記録していくことです。
まず、左下の角からスタートして、一番左の列の下から順に移動していきます。
左下の角はスタート地点なので、'0' を記録します。
続いて、同じ列で隣の場所に移動していきます。
その際に壁を壊すと記録する値を1増やします。
壁を壊さない場合は同じ値を記録します。

次に、右隣の列に移動します。また、一番下の場所から始めます。
ただ、今度は、下の場所から移動するだけでなく左の場所から移動できるので、下から移動してくる場合と左から移動してくる場合の小さい方の値を記録します。
壁なら1を加えた値を、そうでなければ同じ値を記録するのは同じです。
注意しないとならないのは、反対の方向(上から下や、右から左)から来た方が小さな値を記録できる場合があることです。
値を記録したときに、下の場所や左の場所の値をみて、今いる場所から行った方が値が小さくできるときは、書き換えないとなりません。
書き換えた場所の下や左にも影響が及ぶ場合は、書き換えを繰り返さないとなりません。
次の図で、書き換えられた場所を黄色で強調しています。
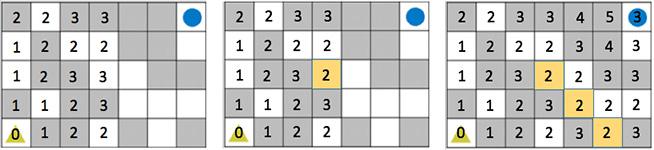
すべての場所に値が記録されると
最終的に、どの場所にも、左下の角からその場所まで移動できるようにするのに壊さないとならない壁の最小値が記録されています。
(右上の角の左隣の場所は、最終的には 4 に書き換えられます。)
右上の角に記録された値は 3 なので、
左下の角から右上の角まで移動できるようにするのに壊さないとならない壁の最小値は 3 となります。 - 実際のコンピュータでは
迷路の脱出経路探索は、情報科学でよく扱われる問題の一つです。
この問題は、壊さないとならない壁をなるべく小さくするという制約が加えられています。
この問題は、左下のかどからその場所までに移動できるようにするのに壊さないとならない壁の最小値を記録しながら、適した方法で探査していくことで解くことができます。
例えば、まず壁を壊さないで行ける場所すべてに 0 を記録し、次に壁を1つ壊せば行ける場所すべてに 1 を記録し、さらに壁を2つ壊せば行ける場所すべてに 2 を記録するということを繰返します。
- 左下の角(かど)から右上の角まで移動できるようにするのに壊す壁(かべ)の最小値は 3 です。

 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は