SeniorAnswer2023

シニア問題解説(高校２年生・３年生)

• A

  2023-お宝からの信号-解説

  • 考案国：スロバキア
  • 正解
    • 5
  • 説明
    • ゲームボード上のマス「C」と「F」が正確であるかを確認するために，マス5までの距離を確認していきましょう。矢印の方向に移動したときにマス5までの距離が増加した場合は「F」が記され，マス5までの距離が減少した場合は「C」がそのマスに記されることが分かります。得られた信号のシーケンスは報告された結果と一致しています。したがって，宝はマス5の下に置かれています。
      
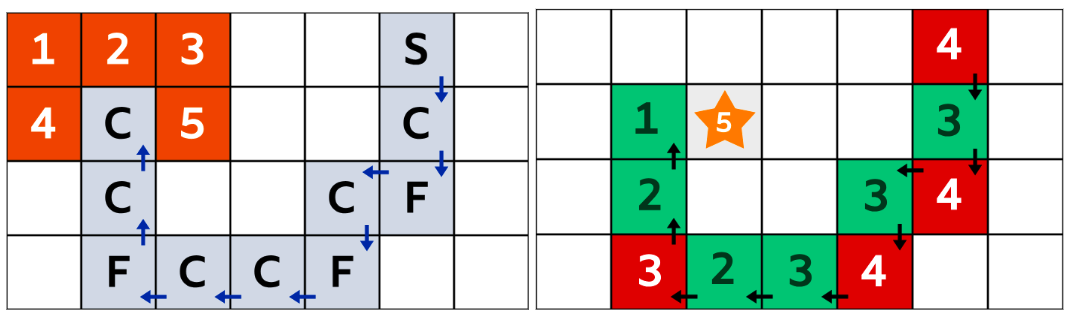
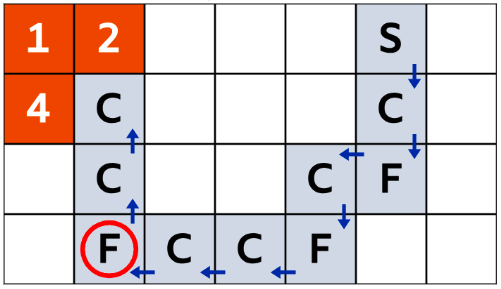
      以下では，他のマスの場合には「お宝の信号」に矛盾が生じてしまうことを検証してみます。
    • マス1、2、または4に埋められた宝の場合：
      もし宝がマス1，2，または4のいずれかの下に埋められていた場合，行4と列2の「F」という文字は「C」でなければなりません。なぜなら，そのマスは宝（これら3つの場所すべて）に近いため，そこから来たマス（行4，列3）よりも近いからです。
      
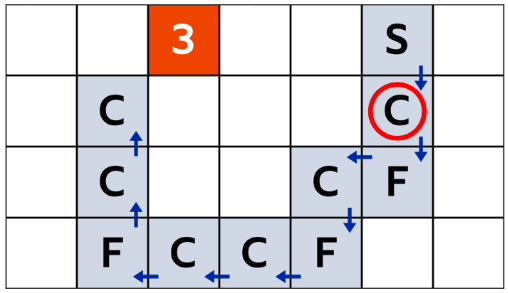
    • マス3に埋められた宝の場合：
      もし宝がマス3の下に埋められていた場合，行2と列6のマスは「F」でなければなりません。なぜなら，そのマスはプレイヤーがスタートしたマス（つまり、行1と列6）よりも宝から遠いからです。
      
  • 実際のコンピュータでは
    • 強化学習は，機械学習の手法の一つで，知的エージェントが環境内で取るべき行動について，報酬を最大化するアルゴリズムです。強化学習システムの基本的な要素には，エージェント，それが相互作用する環境，決定を下すために従う方針，そして行動を取った後に受け取る報酬信号が含まれます。報酬信号を評価するために，評価関数が特定の状態の「良さ」を評価します。
      このタスクでは，移動後のゲームボード上の新しい位置が環境を表し，検出された距離から得られた信号が報酬信号として機能します（'C'は正の報酬を，'F'は負の報酬を示します）。次のステップに最適な決定を下すことで，ビ太郎はエージェントとして機能します。彼は宝が含まれている可能性のあるマスを検討する必要がありますが，これは評価関数と考えることができます。
    • この問題でのマス間の距離は，マンハッタン距離（タクシー距離とも呼ばれる）によって測定され，プレイヤーは水平または垂直にのみ移動できます。自動運転は強化学習の応用例です。予測不能な環境でうまく機能するために，自動運転システムは車両の経路計画や運動予測など，多くの認識と計画のタスクを実行する必要があります。車両の経路計画には，異なる時間的および空間的スケールを考慮した決定を下すためのさまざまな低レベルおよび高レベルの方針の使用が含まれます。一方，運動予測には，歩行者や他の車両の動きを予測し，現在の環境状態に基づいて状況がどのように進化するかについての洞察を提供することが含まれます。

  2023-ウォーキング・ホリデー-解説

  • 考案国：アメリカ
  • 正解
    • 6
  • 説明
    • 
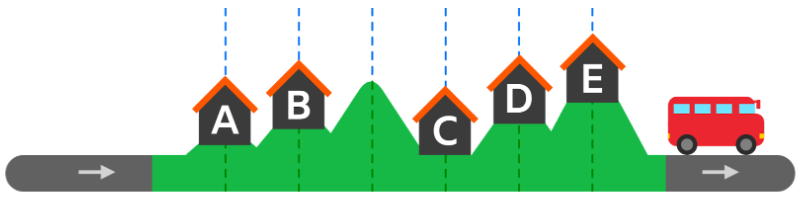
    • 問題を分解して考えることで考えてみましょう。まず，ビバ子はBとCに滞在しなければならないことに気づきます。これらの2つの場所の距離は２であり，ビバ子が1日で歩ける最大の距離だからです。これにより，この前後の二つのセクションを2つの小さな問題として考えることができます。
    • まず，スタートからBまで行く方法について考えます。方法は2つあります（ルート1とルート2に示されている方法）。したがって，Cへの可能なルートも2つということになります。
    • 次に，Cから終点までに行く方法について考えます。これについては，次の3つの可能性があります。
      • C → D → E → End
      • C → E → End
      • C → D → End
    • このようにして，前半で２通り，後半で３通り，合計で2 x 3 = 6つの可能なルートがあることがわかります。
  • 実際のコンピュータでは
    • 説明にあるように，この問題は2つの小さな問題に分解して解決することができます。同様の大きな問題では，動的計画法での解決策が採用されます。アルゴリズムが問題を非常に小さな部分問題に分解し，小さな問題の解決策を使用して大きな解決策を作り出す戦略です。
      
    • タート，A，B，C，D，E，エンドという場所に番号を付けると，各場所に到達する方法が何通りあるかの表を作ることができます。

      場所	到達方法
      スタート	1
      A	1 (スタートから到達できる)
      B	1 + 1 = 2 (スタートから直接来るかAを経由する)
      C	2 (Bから来る必要がある)
      D	2 (Cから来る必要がある)
      E	2 + 2 = 4 (BかCから来る)
      End	2 + 4 = 6 (DかEから来る)

    • 説明でみたように，一つ一つ課題を分割して上記の表を埋めていくことを動的計画法と呼びます。これは，人間が解決するのに時間がかかるような大きな問題に対しても解決策を見つけることができる，コンピュータが得意なアルゴリズムです。

  2023-荷下ろし-解説

  • 考案国：インド
  • 正解
    • 7
  • 説明
    • 荷降ろしの順序は1, 2, 3, 4, 5, 6, 7, 8, 9, 10です。最初のラウンドでボックス1と2が一緒に降ろされ，次に3と4が一緒に，次に5，次に6，その次に7と8が一緒に，次に9，最後に10が降ろされます。これで7ラウンドです。
    • 別の解法として，次に荷下ろしをするコンテナの番号が列車内でそれより左に来る場合，追加のラウンドが必要だという一般原則に気づくかもしれません。例えば，3が2の左に現れる場合，2を降ろすために3はスキップされ，3をクレーンの下に持ってくるために追加のラウンドが必要になります。与えられた課題では，順序が狂っているペアは(2,3), (4,5), (5,6), (6,7), (8,9), (9, 10)であり，6ラウンドの追加が必要なので，合計7ラウンド，と求めることができます。
  • 実際のコンピュータでは
    • 列車内で次に大きい数がそのボックス番号の左にある場合，これを「逆順」と呼びます。このような逆順ごとに，追加のラウンドが必要です。逆順の数を数えると答えが得られます。望ましい順に対して逆順を考える方法には多くの応用があります。例えば，バブルソートなどのいくつかのソートアルゴリズムでは，逆順の数は与えられたシーケンスをソートするために必要な交換の回数を教えてくれます。他の例として，オンラインショップで２名のユーザが商品を好みの順にランク付けした場合，彼らのランキングの逆順の数によって，彼らの好みがどれだけ一致しているかを調べることができます。これはオンラインショップによって「似たような」ユーザを特定し，製品の推薦を行うために使用されます。
    • この問題を解決するためにアルゴリズム的思考が必要です。荷降ろし手順のステップのシーケンスが与えられ，荷降ろしがどれだけ時間がかかるかを決定するためにこれらの手順に従う必要があります。または，解法で見たように，分解と論理を組み合わせたこのタスクの解決方法もあります。

  2023-植物の相性-解説

  • 考案国：オーストリア
  • 正解
    • 
  • 説明
    • まず，にんにくの隣には相性の悪い豆を植えることはできないので，豆はにんにくの植え込みの隣にならない４箇所に植えるようにします。
      
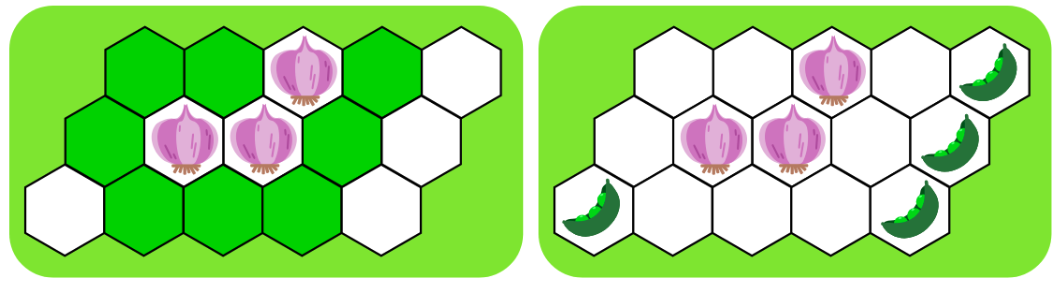
    • 次に，豆と相性の悪いトマトを豆の隣に植えないようにしないといけません。豆の隣を避けるようにすると，トマトを植える３箇所が決まります。
      
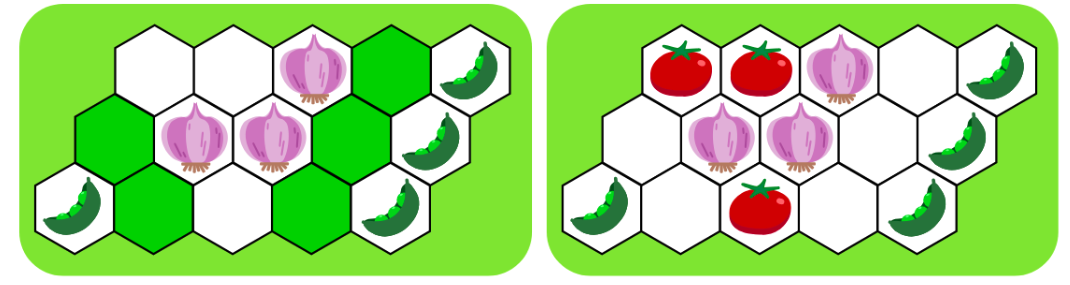
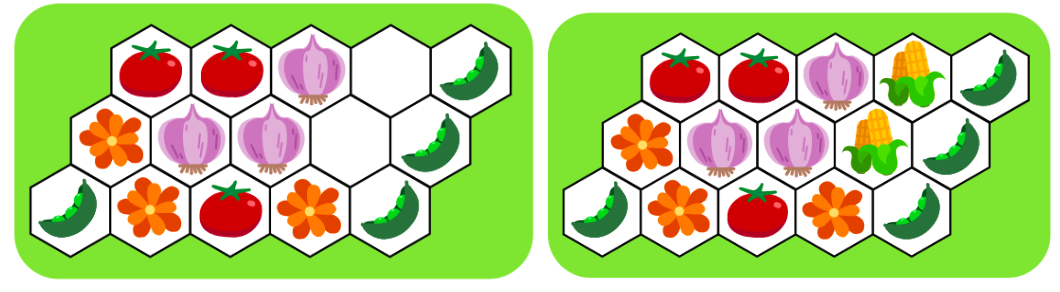
    • 残っているのは3つの花と2つのトウモロコシです。どちらも豆との相性はよく，トマトは花（ミツバチを引き寄せる）との相性が良く，トウモロコシとは相性が悪いです。そのため，トマトの隣には花を植えます。最後の2つのマスには、トウモロコシを植えます。
      
  • 実際のコンピュータでは
    • この問題は多くの方法で解くことができます。全ての条件を満たすまで各植物を全ての植え込みに配置してみるブルートフォース（総当たり/しらみつぶし）アプローチを使用することもできますが，この方法は多くの時間がかかります。代わりに，問題をより分析し，選択の数を減らす条件を探します。
    • 植物間の関係は無向制約グラフで表現できます。二つのノードがエッジ（辺）で接続されているのは，それらが良い共栄作物である場合（緑の実線），もしくは相性が悪い作物である場合（赤い点線）です。
      
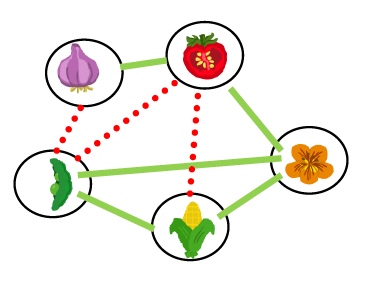
    • この問題は，決定問題の1つとして知られる組み合わせ最適化問題でもあります。多くの組み合わせ最適化問題は，グラフ問題としてモデル化し，グラフ問題の最適化，what-if シミュレーション，制約充足問題，グラフ分類，グラフ描画と可視化などで解決します。
    • 農家や他の園芸家は，庭に植生を植える際に共栄作物の情報を使用します。この情報は，庭の生産を最適化するための情報に基づいた決定を下すのに役立ちます。例えば，豆は窒素を提供することでトウモロコシに利益をもたらし，トウモロコシの植物は安定性を提供することで豆を助けます。
• B

  2023-オガム・コード-解説

  • 考案国：アイルランド
  • 正解
    • 
  • 説明
    • 答え見つけるためのさまざまな方法がありますが，以下では，1つの例を示します。
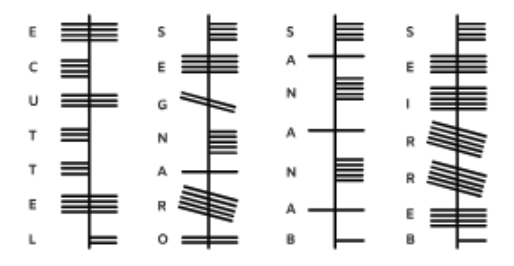
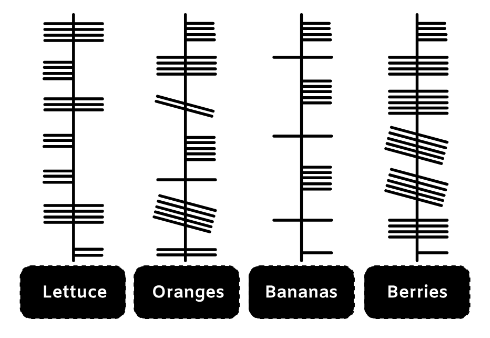
    • 最初のステップは，単語をどの方向で読むかを解読することです。左から右へ（または右から左へ）ではないことは直感的にわかります。なぜなら，その場合，単語は4文字で，7つの単語に鳴るはずだからです。各ボックスの位置も意味をなさなくなります。そこで，まずは上下の4つの文字と，単語の最初と最後の文字を比較します。3つの単語が同じ文字（S）で終わるため，それらは上で終わらなければならないので，読み方は下から上，ということがわかります。ここまでわかったら，各単語を個別に分析します。
      • BANANASは3つの同じ文字「A」を持つ唯一の単語であり，3番目の画像も3つの同じ文字を持っているので，それはBANANASでなければなりません。したがって，文字Aは単一の長い線であることがわかります。
      • ORANGESは「A」を持つ他の唯一の単語です。残った唯一の画像には単一の長い水平線がありますので，2番目の画像は「ORANGES」でなければなりません。
      • 残りの単語はLETTUCEとBERRIESです。
    • ORANGESとBANANASの両方が「S」で終わります（右に4つの水平線）。4番目の画像も同じ文字で終わるので，それはBERRIESでなければなりません。 したがって，LETTUCEは最初の画像ということになります。
    • 最終的な各文字の解釈を以下に示します。
      
  • 実際のコンピュータでは
    • この問題は暗号解読の簡単な例を扱っています。暗号解読は，暗号を「解読」する方法に関する研究です。暗号解読は，暗号を複合するのに必要な「鍵」がない状態で，暗号化されたメッセージを解読するのに使用されます。暗号解析家と呼ばれる専門家がメッセージを解読しようとします。その際、彼らは隠されたメッセージにおそらく含まれているであろう単語についての知識を使用します。
    • パターン認識： この問題を解くには，単語と絵の間のパターン（同じ文字の繰り返しなど）を見つけることが重要です。
    • 分解： この問題は，解読できる部分に分割することで解くことができます（例えば，一度に1つの文字を見つけ出す）。部分的な解答を組み合わせることで，最初は複雑だった問題を解くことができます。
    • 表現： この問題では，文字がどのように異なる記号や絵で表されるかを理解する必要があります。

  2023-採用-解説

  • 考案国：イラン
  • 正解
    • Yunas は倉庫担当に採用されます。
  • 説明
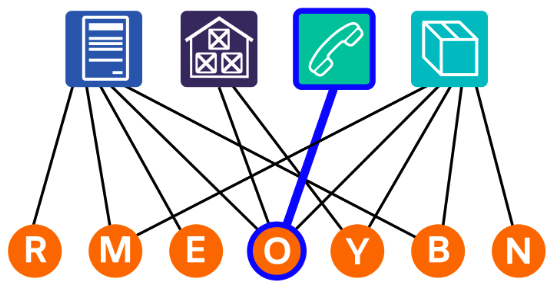
    • ある仕事に1人しか応募者がいない場合，その応募者は他の仕事にも応募している場合でも，その仕事に採用される必要があることに注意する必要があります。Omran はただ一人のコールセンター担当応募者なので，Omran をコールセンター担当で雇われなければなりません。 したがって，「Omran は梱包担当に採用されます。」は誤りです。
      
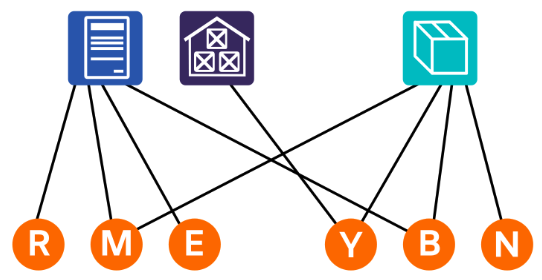
    • すると，コールセンター担当の仕事は Omran に決まり， また， Omran は１つの仕事しか持てないので，Omran とコールセンター担当とそれらに接続している線を図から取り除きます。
      
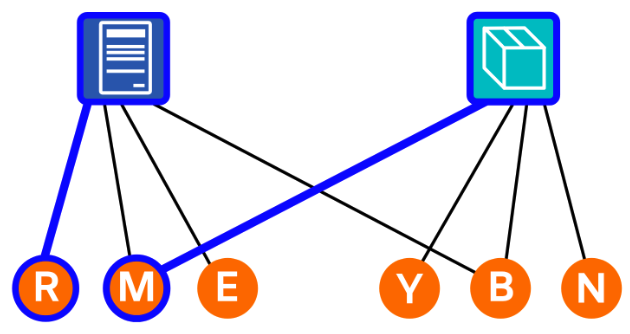
    • 更新された図の Yunas に対して同じ考えを適用すると， Yunas は倉庫担当として採用され，「Yunas は倉庫担当に採用されます。 」が正しいことが分かります。
      
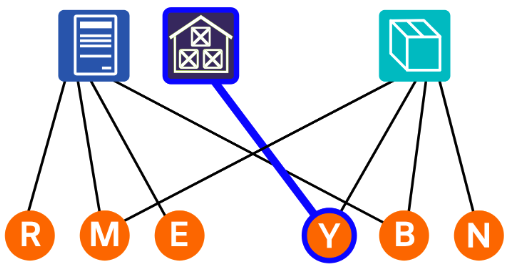
    • Yunas と倉庫担当を及びそれらに接続している線と取り除くと，他の選択肢が正しくないことが明瞭に分かります。
      
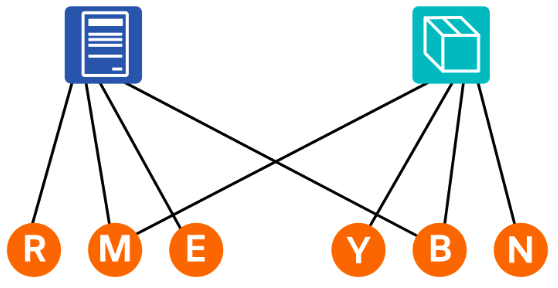
    • 例えば， Mary は梱包担当として，Elif は経理担当として採用されるかもしれません。
      
  • 実際のコンピュータでは
    • この問題は制約充足問題であり，変数に値を割り当てることで他の選択肢を排除し，集合論の記法を用いて表現することができます。例えば，仕事の割り当てを適用する前の倉庫担当 = {Omran, Yunas} などです。制約充足問題は，実世界での資源割当て問題やパズル（数独など）で使われています。
    • また，この問題では，仕事と応募者のデータ構造を表現するために二部グラフを使用しています。二部グラフは二つのカテゴリ(部集合）の頂点を使用したグラフ表現です。ノード（頂点）のマッチング問題は，入力を二部グラフに限ると，多項式時間アルゴリズムが存在します。

  2023-ビバ子の買い物-解説

  • 考案国：ベルギー
  • 正解
    • 39分
  • 説明
    • 正解は39分です。最短時間でのルートは以下の通りです：
      • エマの家 → 学校 → 薬局 → 学校 → 教会 → パン屋 → 鍛冶屋 → パン屋 → 市場 → エマの家
    • これには6 + 3 + 3 + 4 + 4 + 3 + 3 + 6 + 4 = 36分が必要で，買い物に3分 = 合計39分です。彼女はこの道を逆方向にたどっても同じ時間がかかります。
    • より短いルートがないことを確認するために，地図の簡略版を使用します。
      • 下の図をご覧ください：
        
        丸印（ノードや頂点と呼びます）は村の異なる場所を表し，線（エッジや辺と呼びます）はそれらの間の道を表します。地図にあるように，各エッジの隣の数字は，その道を歩くのにかかる時間を示しています。
      • 灰色のエッジは無視できます（下図参照）。中間ノードを経由するより速いルートがあるからです。
        
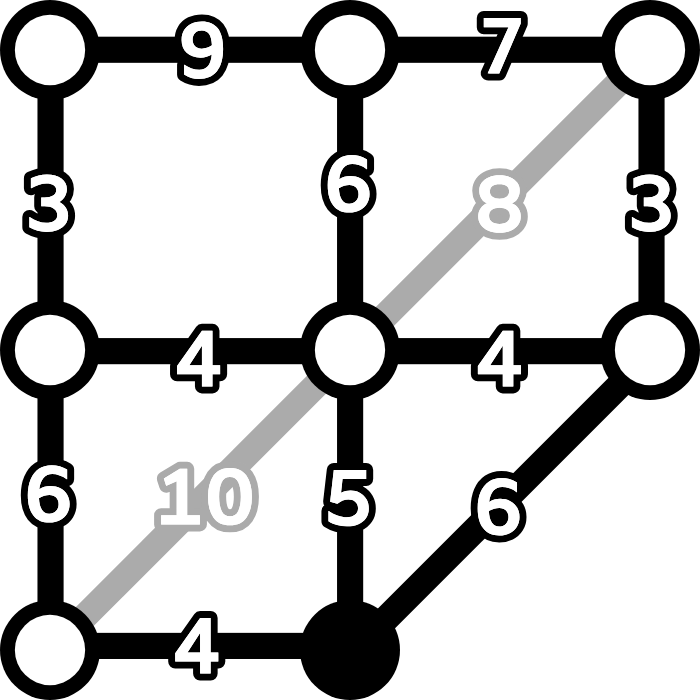
      • 「公園」のノードも無視できます。公園でのタスクがなく，公園を通るすべてのルートにはより速い代替ルートがあるからです。
        
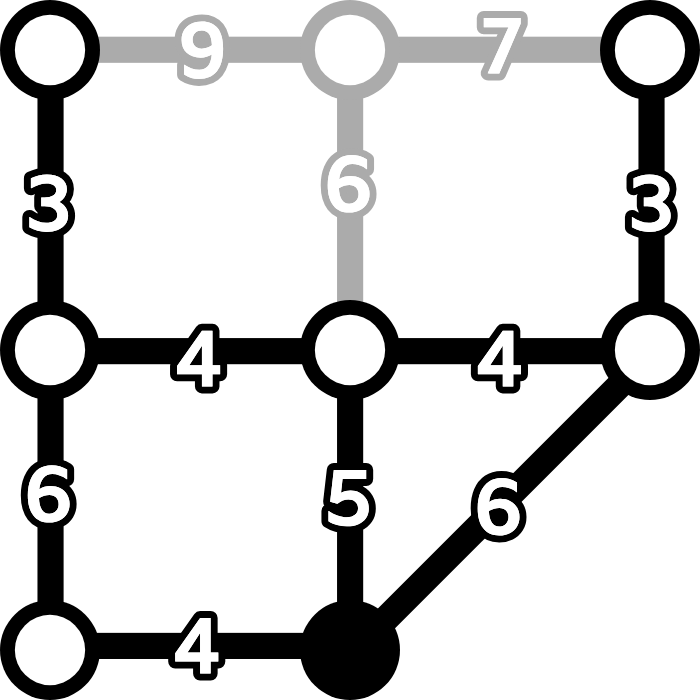
      • 残った図の上部にある2つのノード（鍛冶屋と薬局）はビバ子が訪れる必要があります。これは常にその直下のノードを通って行われ，どちらの場合もそこまで3分，戻るのに3分かかります。
      • これらのノードを取り除き，最終結果に12分を追加することを覚えておきます。
        
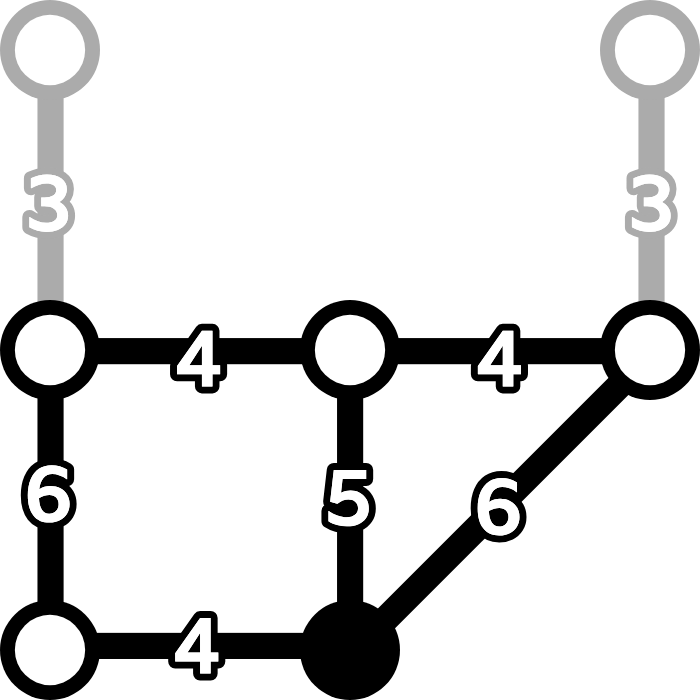
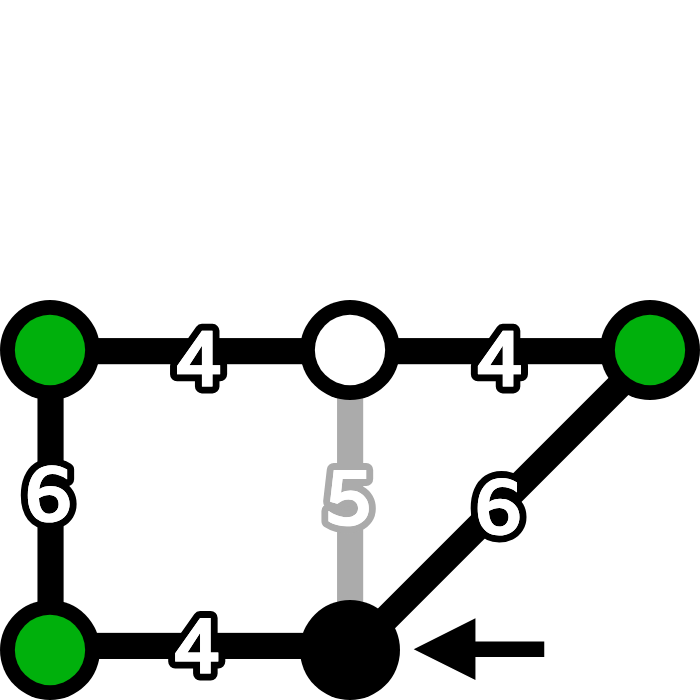
      • 最終的に右図のようになります。矢印がある右下のノードで始めて終わり，3つの色付きノードをすべて訪れる必要があります。最短のルートは，灰色に塗られたエッジを除いて5つのノードを通ります。
      • このルートには4 + 6 + 4 + 4 + 6 = 24分かかります。前のステップからの12分と各訪問地でのタスクを完了するのに3分を加えると，合計時間は39分になります。
        
  • 実際のコンピュータでは
    • 最短ルートを見つけるために使用した簡略化された図は，グラフと呼ばれます。コンピュータサイエンスの多くの問題は，このようにグラフを作って，解析することで解かれます。この問題では，グラフ内の特定のノードを通る最短経路を見つけようとしています。
    • コンピュータは「最短経路」問題をもっと多くのノードとエッジを持つ場合に使用されます。例えば，交通や流通の問題で，ゴミ収集車，郵便配達員，または牛乳配達車が巡回する最短経路を計算するために使用されます。
    • 問題をモデル化するためにグラフを使用することは，抽象化と呼ばれます。私たちは様々な場所の名前やそれらを結ぶ道の形状については（ここでは重要ではないので）考えないようにして（捨象，といいます），どの場所がどの場所とつながっているか，とそれらの移動にかかる時間に集中して考えます。この抽象化が問題の解決に役立ちます。
    • 地図自体も村を抽象化したものです。このように，抽象化という概念を知ったり，使ったりすることも，計算論的思考 (Computational Thinking) の一部です。

  2023-ジューススタンド-解説

  • 考案国：ブラジル
  • 正解
    • 4
  • 説明
    • 追加のジュースカートの最適な場所を見つけるために，まず，既存のジューススタンドから１つか2つの道路を歩いて行ける交差点をすべて除外します。
      
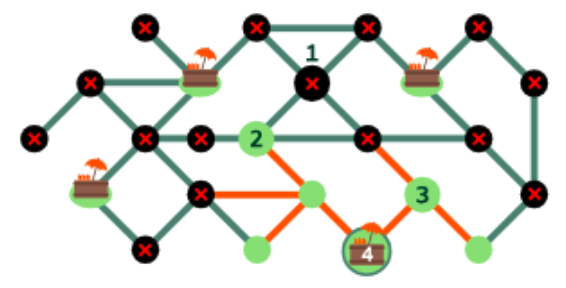
    • 除外すると，2つの通りを歩いてジューススタンドにたどり着けない場所は，4つの交差点のみになり，問題は単純になりました。交差点1, 2, 3 にジュースカートを配置しても，1つか2つの通りでジューススタンドに到達できない場所がまだいくつか残ります。交差点4にジューススタンドを配置すると，残りの各交差点が最大で2つの通りの距離になります。
  • 実際のコンピュータでは
    • グラフは，地図上の通り，人々の関係，閉じたシステム内の状態，階層的に整理された単語など，さまざまな文脈に適用することができます。この問題は，グラフ理論での「支配集合問題」を扱っています。この理論は，この問題の例のように，最大2回の移動で全ての市民や場所にサービスを提供する公共交通網をどのように構築するかといった，実世界の問題に適用されています。
• C

  2023-橋をかける仕事-解説

  • 考案国：ニュージーランド
  • 正解
    • 
  • 説明
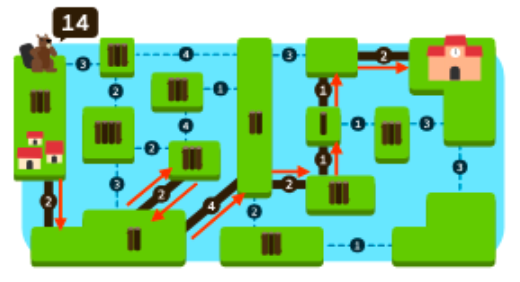
    • 　各ステップで拾った丸太の累積数と使用した丸太の累積数を記録することで，正しい経路が実行可能であること（各ステップで拾った丸太数 ≥ 使用した丸太数）を示すことができます：(3,2)(5,4)(8,4)(8,8)(10,10)(13,11)(14,12)(14,14)。
    • 丸太の使用数が14本以下のケースで，村と学校を結ぶ全ての経路を見つけ，上記の正しい回答だけが実現可能であることを示すことで，これが最小であることを証明することができます。まず，すべての経路が中央の大きな島を通る必要があるため，問題を二つの部分に分けることができます。次に，村から中央までの経路には少なくとも6本の丸太が必要であり，中央から学校までの経路には少なくとも5本が必要です（これを下界と呼びます）。
      
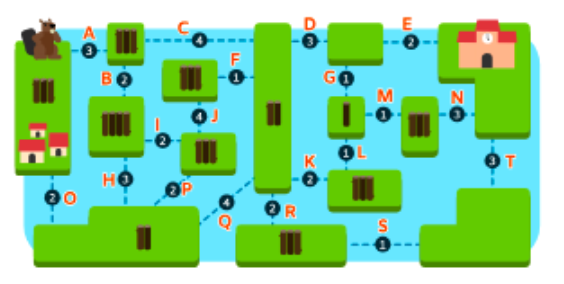
      まず、右側の下限(5本)を考慮して左側の部分を解決します。右側の下限は5本なので，左側は9本以下の丸太を使用する可能な経路を探すことにします。左側では，以下の経路が中央まで繋がり，9本以下の丸太を使用します（拾った丸太，使用した丸太）。
      {A,C}=(6,7),{A,B,C}=(10,9),{O,Q}=(5,6),{O,H,Q}=(9,9),{O,P,Q}=(8,8),{O,P,J,F}=(11,9)
      「拾った丸太 < 使用した丸太」となった実現不可能な解決策を除去すると，次のようになります。
      {A,B,C}=(10,9),{O,H,Q}=(9,9),{O,P,Q}=(8,8),{O,P,J,F}=(11,9)
      次に，左側で8本の使用丸太を下限として右側を解決するため，6本以下の丸太を使用するすべての経路を探します。
      {D,E}=(2,5),{D,G,E}=(3,6),{K,L,G,E}=(6,6),{R,S,T}=(5,6)
      左側と右側の解決策を組み合わせて，合計で14本以下の丸太を使用する可能性のある組み合わせを探すと，{O,P,Q}=(8,8)+{K,L,G,E}=(6,6) → (14,14) となります。
  • 実際のコンピュータでは
    • この問題での陸地と橋は，グラフ理論でのノードとエッジとして表現することができます。各陸地で拾われたり，橋を建設するために使われる丸太の数は，それぞれのノードとエッジに割り当てることができます。
    • この問題を一般的に解決するには，資源制約付きの経路探索アルゴリズムを使用することができます。すべての有効な経路を徹底的に検索する力任せの方法も有効ですが，計算時間はグラフのサイズが大きくなるにつれて指数関数的に増加します。
    • 別の方法として，この問題の解法が示すように，分割統治法として考えることもできます。このアプローチは，パス整合性や分岐限定法などの制約最適化の技術を使用します。これらの技術は，実世界の資源配分問題，パズル（例えば数独のような），およびゲームプレイ人工知能などの基礎となっています。

  2023-電子錠-解説

  • 考案国：ウクライナ
  • 正解
    • 74105623
  • 説明
    • nの階乗の組み合わせがある全ての組み合わせのパスワードを試して，手動でパスワードを得ることは現実的ではありません。迅速な解決策へのヒントは，最小の数字（数字 0）から最大の数字（数字 8）まで，数字を左から順にその場所に置く必要があるということです。
      1. 0>>3 から、数字 0 の左には3つの空きセルがあることがわかります。つまり、数字 0 は左から4番目のセルに確実にあるということです。
      2. 1>>2 から、数字 1 の左には2つの空きセルがあることがわかります。つまり、数字 1 は左から3番目のセルに確実にあるということです。
      3. 2>>4 から、数字 2 の左には4つの空きセルがあることがわかります。つまり、数字 2 は左から6番目のセルに確実にあるということです：

         1

         0

         1

    • 残りの5桁も同じように考えていくことで，新しいパスワードとしてふさわしい選択肢がわかります。
  • 実際のコンピュータでは
    • 全ての可能な順列を生成し，正しいものだけを見つけることは，組み合わせ論，情報符号化，暗号学の古典的なアルゴリズムに属します。組み合わせ論では，与えられた数より左にある大きな数の量を逆数と呼びます。
    • 解決策に到達するために値の割り当てを順次適用することは，制約満足度のための弧整合性アルゴリズムの例です。このアルゴリズムは，多くの実世界のリソース割り当て問題や，数独のような人気のパズルの解決策の基礎を形成しています。

  2023-逆ポーランド記法-解説

  • 考案国：オランダ
  • 正解
    • 
  • 説明
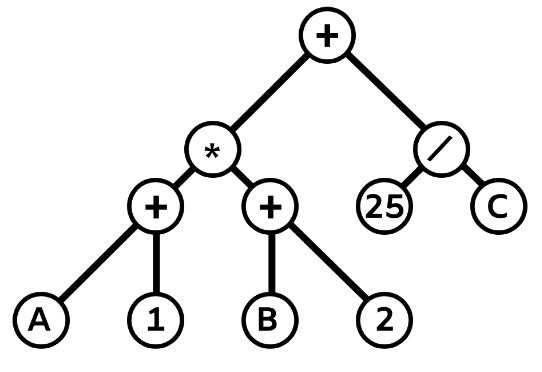
    • A 1 + は次のように表現されます。 .
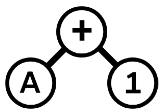      B 2 + は次のように表現されます。 .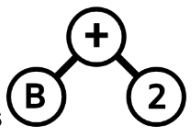
      A 1 + B 2 + * は次のように表現されます .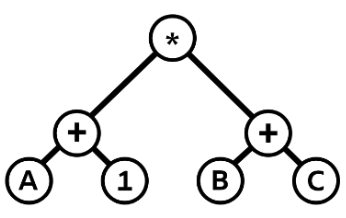
      25 C / は次のように表現されます。 .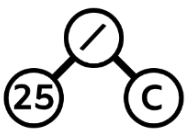
    • したがって， A 1 + B 2 + * 25 C / + は次のようになります。.
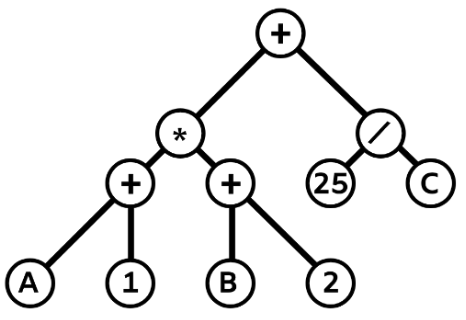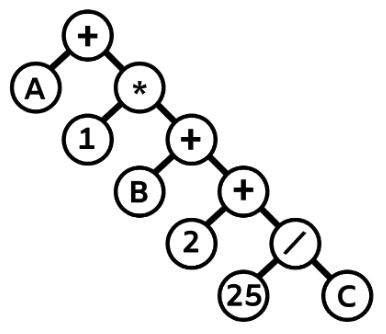    • は不正解で， A 1 B 2 25 C / + + * + の表現となります。
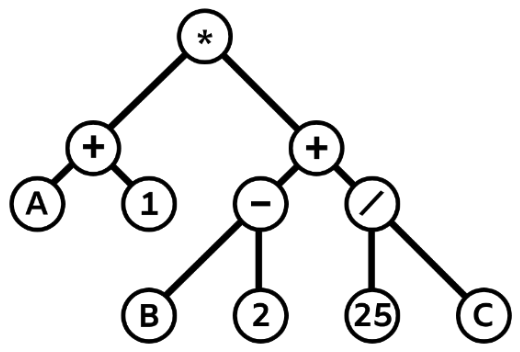    • も不正解で，元の式にはないマイナス記号が含まれています。
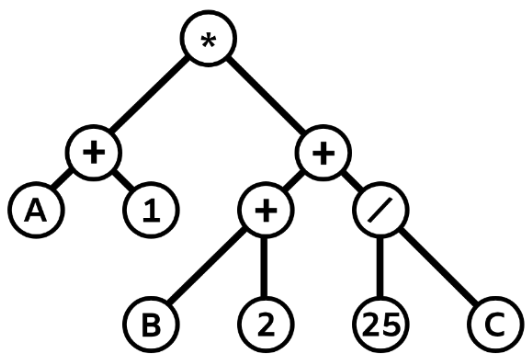    • も不正解で， A 1 + B 2 + 25 C / + *　の図となります。
  • 実際のコンピュータでは
    • 　逆ポーランド記法は，コンパイラが内部で使用する形式です。コンパイラは，プログラミング言語をコンピュータが理解できる機械コードに変換する仕組みです。コンパイラは，中置記法（３＋５など）で書かれた形式の式を逆ポーランド記法（３　５　＋）に変換して処理を行います。逆ポーランド記法では，演算子が最後に来るので，後置記法とも呼ばれます。
    • 情報科学の分野では、しばしば木構造が抽象データ型として使われます。木構造の中の各ノードは、1つの親と複数の子とつながっています。子をふたつずつ持っている木構造を二分木といいます。数式は、演算子（＋，×など）一つに対してと被演算子（５，３など）を2つずつもつ二分木に関連付けることができます。

  2023-異なる意見の検出器-解説

  • 考案国：ドイツ
  • 正解
    • 
  • 説明
    • 正解は２つあります。
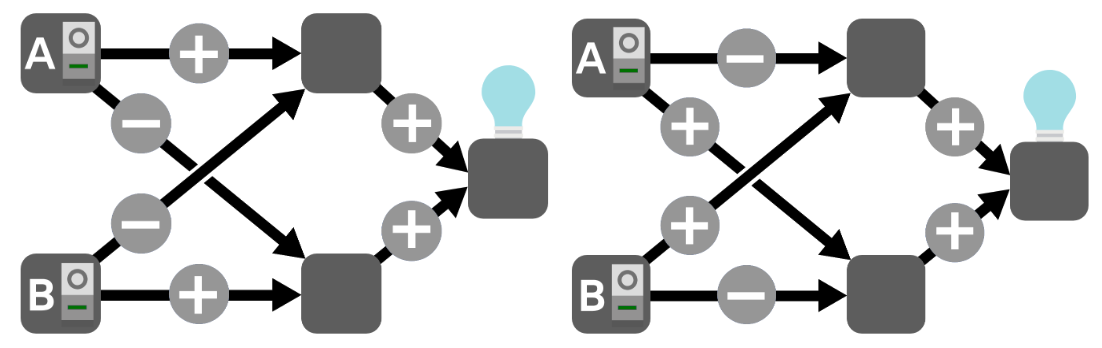
    • 2つの判定ボックスのうち，1つは A が YES 状態で B が　NO　状態のときに　YES　状態になり，もう1つは A が NO 状態で B が YES 状態のときに YES 状態になります。2つの判定ボックスのいずれかが YES 状態になると，出力ボックス（ランプ）の状態も　YES　に設定されます。したがって，ビバ子とビ太郎の意見が異なる場合に限り，ランプが点灯します。
    • 次の図では，1つの解法での，可能なすべての入力の組み合わせに対してのワイヤとボックスの状態を示しています。

      "A: YES, B: NO"	"A: NO, B: YES"	"A: YES, B: YES"	"A: NO, B: NO"

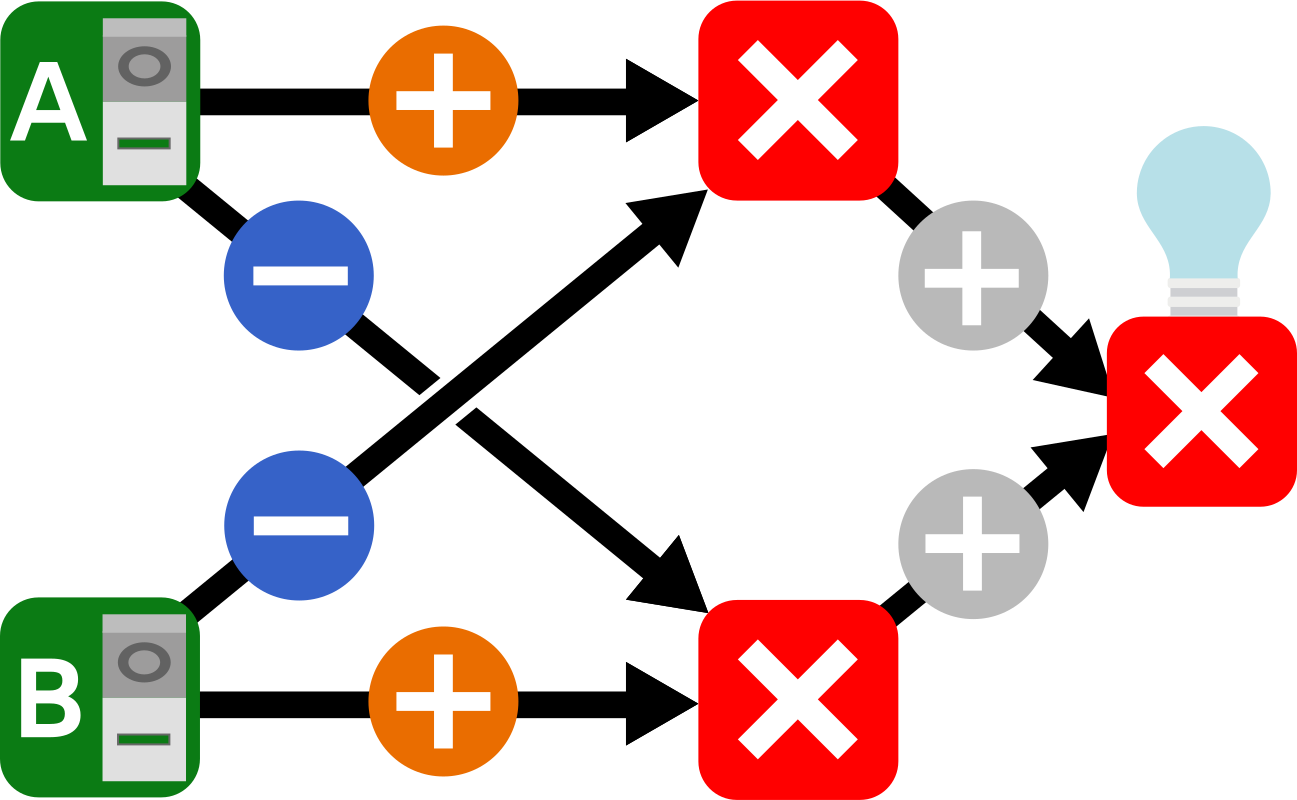
  • 実際のコンピュータでは
    • 「異なる意見の検出器」は，2つの YES/NO 入力を取り，2つの入力が異なる場合に限り YES と評価します。この機能は XOR （排他的論理和）と呼ばれます。これは，どちらか一方の入力だけが　YES　の場合に限り，かつ，両方が YES でない場合に YES と評価するためです。
    • YES， No の入力値は通常，真(True)/偽(False)と呼ばれ，それらを処理する関数は論理演算子と呼ばれます。論理演算子はすべてのコンピュータの基盤です。
    • 排他的論理和 (XOR) は，入力のいずれかが真の場合（一方が真で他方が偽）に真と評価される論理演算子です。一方の入力が真で他方が偽の場合に限り真となります。条件式の様々な入力の真/偽の状態に関係なく，異なっているかどうかだけを見極めようとするとき，排他的論理和は非常に有用です。
    • YES/NO ユニットのネットワークは，簡略化された多層パーセプトロンです。パーセプトロンは，1957年にフランク・ローゼンブラットによって提案された単純なタイプの人工ニューラルネットワークです。XOR 関数を実装するために入力と出力の間に追加の層が必要という事実により，人工ニューラルネットワークの可能性は長年保留されてきました。しかし現在では，人工ニューラルネットワークは，例えば画像処理などの機械学習技術で一般的に使用されるようになっています。通常，接続の重み（このタスクでは負の接続と正の接続のより一般的なケース）は手動で選択されることなく，正しい出力が与えられる教師データから自動的に学習されます。

（シニア問題に戻る）