SeniorAnswer2018
シニア問題解説(高校2年生・3年生)
- A
2018-スケジュール-解説
- 考案国:インドネシア
- 正解
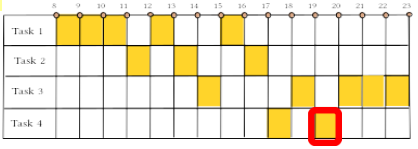
- 説明
- コンピュータになったつもりで、ルールのとおりに色を塗っていきましょう。
- 実際のコンピュータでは
- コンピュータは「文字の入力」「日本語変換」「ネットワーク通信」「時刻の表示」などの複数の処理を、細かく処理を分割することで並行して行っています。ひとつの処理だけに時間を使って他の処理が止まらないように、全体の処理のバランスを取ることは重要です。
2018-矢印-解説
- 考案国:ハンガリー
- 正解
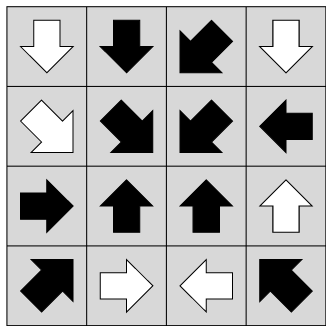
- 説明
- 条件を満たす解を見つけるため、ある矢印から始めて、仮に白か黒に決め、その矢印が指している矢印の色を条件を満たすように仮に決める(複数の可能性がある場合は、そのうちの一つを選び)ということを繰り返し、うまく選べなくなったら複数の可能性から選択した矢印まで戻り、まだ試してない可能性を選択するという方法があります。戻ったとき、もう選ぶ選択肢がない場合は、さらに戻ります。
- このように、ある状況から可能性を探索し、ステップバイステップで進み、行き詰まるともとに戻る方法を、情報科学ではバックトラックと言います。 バックトラックは、8クイーンパズルや数独などのパズルを解くのに、また,ナップザック問題などの組み合わせ最適化問題を解決するのにも使用できます。他にも、様々な応用があります。
https://ja.wikipedia.org/wiki/バックトラッキング
https://ja.wikipedia.org/wiki/論理プログラミング
2018-関係-解説
- 考案国:カナダ
- 正解
- 「5」
- 説明
- まず、上段中央の「=4」の円に注目します。この円とつながっている円はちょうど4つなので、つながっている4つの円全てに色を塗りましょう。
- 次に、右下の「=2」の円に注目します。この円とつながっている円はちょうど2つなので、つながっている2つの円に色を塗りましょう。
- すると下の図のようになります。この図で、残りの円の条件を見ていくと、すべての条件が満たされていることがわかります。よって、この時点で塗られた5個の円が正解になります。
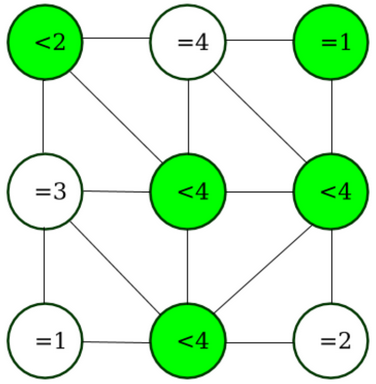
- 実際のコンピュータでは
- いろいろな組み合わせが考えられる問題を、手当たり次第に解くと時間がかかってしまいます。この問題には9個の円がありましたので、すべての組み合わせを考えると512通りについて考えなければなりません。そこで、今回の解法のように、調べる組み合わせの候補を少なくする工夫が行われています。
2018-手旗信号-解説
- 考案国:台湾
- 正解
- 「QPPTP」
- 説明
- 「水平を0、垂直を1」で表すと、次のようになります。
問題 :10010010
RPQSR:100100110
RPSP :1000010
QPPTP:10010010
TSQ :10010011
- 「水平を0、垂直を1」で表すと、次のようになります。
- 実際のコンピュータでは
- コンピュータは2進数で動くため、文字も0と1の組み合わせで表現しています。どの文字にどのような0と1の組み合わせを割り当てるかは重要です。この問題のように「S(10)はQ(1)とP(0)の並びとも解釈できる」ような割り当てにすると、解釈に曖昧さが生まれてしまいます。実は、選択肢にはありませんが、TSP (10010011) も問題の図の信号になります。
- B
2018-行と列-解説
- 考案国:ベルギー
- 正解
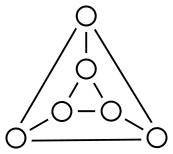
- 説明
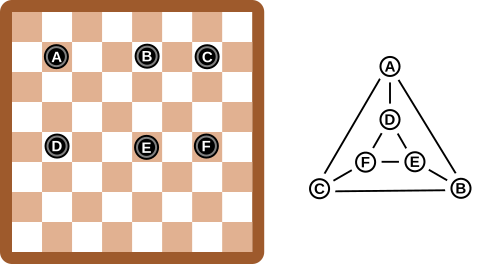
- 考えやすくするために、円に文字を振りましょう。そうすると、上の3個は同じ横一列にありますので、「AとB」「BとC」「AとC」が線でつながります。下の「DとE」「EとF」「DとF」も同じです。そして、縦に「AとD」「BとE」「CとF」がつながります。このような形です。

- 選択肢にはこのような形はありませんが、選択肢の中から「3個がそれぞれつながっている」形が2組あり、それらが3本の線でつながっている形を探すと、次のものが正解になります。
- 考えやすくするために、円に文字を振りましょう。そうすると、上の3個は同じ横一列にありますので、「AとB」「BとC」「AとC」が線でつながります。下の「DとE」「EとF」「DとF」も同じです。そして、縦に「AとD」「BとE」「CとF」がつながります。このような形です。
- 実際のコンピュータでは
- コンピュータでは、解きたい問題を点と線で表す「グラフ」と呼ばれるデータ構造を使うことがあります。グラフでは、この問題のように、「どの点とどの点が線でつながっているか」は重要ですが、その配置は意味を持ちません。
2018-カードゲーム-解説
- 考案国:ベルギー
- 正解
- 「101ステップ以上1000ステップ以下でできる」
- 説明
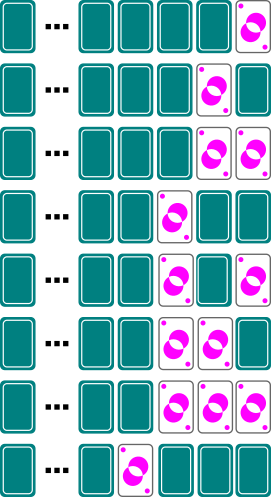
- まず、最初の何回かを試してみましょう。すると、次のような結果になります。ここで、「1枚だけが表になっている」パターンに着目すると、「1回目、2回目、4回目、8回目」であることがわかります。そうすると、次に「1枚だけが表になっている」のは16回目であることが推測できます。そして、「1枚だけが表になっている」パターンの直前は、「表になっている1枚より右のすべてが表になっている」状態であることがわかります。
- そう考えると、7枚のカードがすべて表になるのは、右から8枚目のカードが「1枚だけ表になっている」状態(128回目)のひとつ前(127回目)になります。
- 実際のコンピュータでは
- コンピュータは0と1の組み合わせで数を表す二進法を使い、さまざまな数を扱っています。この問題では二進法の7桁でいくつの数を表現できるかを扱いました。
2018-短いプログラム-解説
- 考案国:イギリス
- 正解例
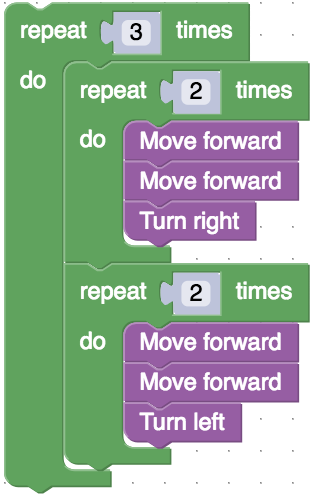
- 説明
- 解答を得るアプローチを1つ示しましょう:
- まずは、ブロックの数が多くても良いのでゴールに到達できる単純なプログラムを作成します。
- 次に、同じブロックのパターンを繰り返している部分を repeat でまとめて、使用するブロックの数を減らします。これを何度か繰り返します。
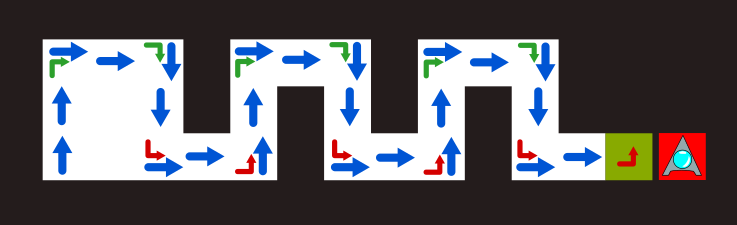
- 道順によっては、使用するブロックの数を十分小さくできないこともあるでしょう。この迷路の場合は、スタートのあたりは道順がいろいろと考えられますが、図1のように、途中からは一本道です。途中からの道順を良く観察して解析すると、図2のようにパターンを繰り返せば良いことが分かるでしょう。
- 図2の道順で進むことにして、単純なプログラムをつくって見ましょう。図3・図4のようにまとめられそうなブロックのパターンを見つけます。
図1 図2 

図3 図4 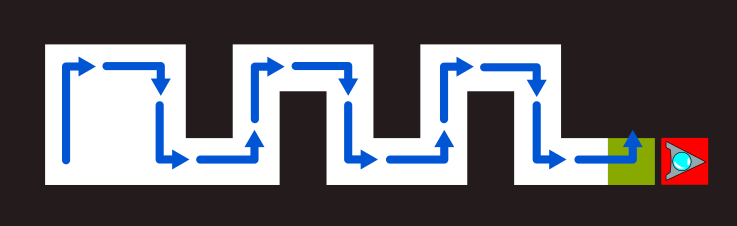
- 解答を得るアプローチを1つ示しましょう:
- 実際のコンピュータでは
- この問題では、繰り返されているパターンを見つけて、問題を解決しました。
これは、プログラマのコードをタイプする手間を節約するだけでなく、エラーがあった場合にそれをすばやく修正するのにも役立ちます。
繰り返しを活用しなければ、この問題では29個のブロックを使用する必要があります。 - 情報科学やプログラミングにおいて、パターンにうまく抽出することは、あるタイプの問題に対する適切な解決方法を知る上で重要です。パターンや類似の特性に気づくことで、解決法の道筋を見つけ、問題を解決できます。
- この問題であなたが発見した繰り返しのパターンは、アルゴリズムやプログラムの反復構造になります。
- この問題では、繰り返されているパターンを見つけて、問題を解決しました。
2018-デバッグ-解説
- 考案国:イラン
- 正解
- 「3番目のステップを、6番目の位置(終了直前)に移動する」

- 「3番目のステップを、6番目の位置(終了直前)に移動する」
- 説明
- 登録が完了する前にユーザが作られてしまうと、中途半端なユーザができてしまいますし、同じユーザ名で再度作ることもできなくなってしまいます。そこで、すべての登録作業が正しく行われた後でユーザを作ることが必要です。
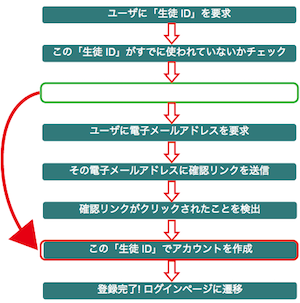
- 登録が完了する前にユーザが作られてしまうと、中途半端なユーザができてしまいますし、同じユーザ名で再度作ることもできなくなってしまいます。そこで、すべての登録作業が正しく行われた後でユーザを作ることが必要です。
- 実際のコンピュータでは
- プログラムのミスを発見して修正することを「デバッグ」といいます。デバッグは、プログラム開発の重要な作業のひとつです。この問題では、「必要な処理がすべて成功したら登録する」「完了しない処理がひとつでもあれば登録しない」というトランザクションの考え方を扱っています。
- C
2018-検査-解説
- 考案国:チェコ
- 正解
- 「容器は振られることはない」
- 説明
- プログラムを、1行ずつ指さしながら1行目から動かしてみましょう。まず、1行目でAに0が入ります。次に2行目でAに1が足されます。次に3行目から6行目に処理が移りAに1が足されます。次に7行目から2行目に戻り、Aに1が足されます。
このように、何度も何度もAに1が足されていきますが、8行目が処理されることはありませんので、容器が振られることはありません。
- プログラムを、1行ずつ指さしながら1行目から動かしてみましょう。まず、1行目でAに0が入ります。次に2行目でAに1が足されます。次に3行目から6行目に処理が移りAに1が足されます。次に7行目から2行目に戻り、Aに1が足されます。
- 実際のコンピュータでは
- 1940年代に作られた、アセンブリ言語と呼ばれるプログラミング言語では、行に番号が付けられて、次の処理をどの行に移すのかを "go to" の形で記述していました。このようなプログラミング言語で、プログラムを書くことは難しくありませんが、処理を追って動作を確認することは難しく、大きなプログラムを書くのには適していません。現在では "go to" を使わない、構造化された言語が良く使われています。
2018-ダンスフロア-解説
- 考案国:アメリカ
- 正解例
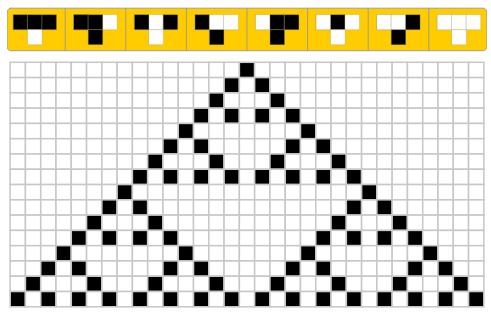
- 説明
- ルールの上部にある3個のタイルの白と黒の組み合わせは 2*2*2 = 8通りです。それぞれに対して、下部のタイルを白か黒にするので、ルールとなる組み合わせは全部で 2*2*2*2*2*2*2*2 = 256通りあります。その中の16通りが、オーナーの希望を叶えるルールとなります。
- 上の正解例は「XOR」の考え方を利用しています。上部の真ん中のタイルを無視して両端のタイルだけに着目し、「上段の両端のタイルが同じ色なら、下段のタイルは白」「上段の両端のタイルが違う色なら、下段のタイルは黒」と考えると、正解のルールになります。
- 例えば、次の図も16通りある正解の1つです。

- 残りの正解はどのようなルールか考えてみましょう。
- 実際のコンピュータでは
- この問題では、Conwayが考案したセル・オートマトンを扱っています。いくつかの単純なルールから、複雑なドット絵のパターンを扱えるライフゲームを作ることができます。
2018-リハーサル-解説
- 考案国:ベルギー
- 正解
- 「Chloe」
- 説明
- バレリーナのデュエットの関係を次のように図で表してみましょう。バレリーナを円で表し、デュエットを踊る2人のバレリーナの円の間を線で結びます。
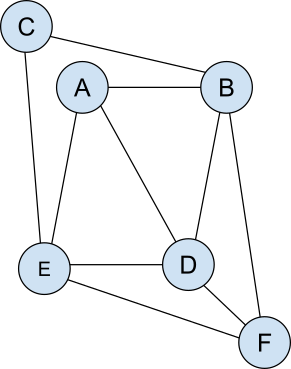
- バレリーナのどちらかは次のデュエットを踊り、その上、同じバレリーナが3回連続踊ることがないことから、最初の組で踊って次は踊らないバレリーナの円からスタートして、全ての線をちょうど1回ずつ辿れるはずです。(線は2人のバレリーナを結んでいるので、線を辿る順にその線の2人でリハーサルを踊ります。)
- そのためには、最初と最後以外のバレリーナは偶数本の線で結ばれている必要があります。このことから、最初と最後のバレリーナはAかFとなります。AともFともデュエットを組まないバレリーナはCだけです。
- バレリーナのデュエットの関係を次のように図で表してみましょう。バレリーナを円で表し、デュエットを踊る2人のバレリーナの円の間を線で結びます。
- 実際のコンピュータでは
- データの関係を点と線で表す「グラフ」構造で表現することができます。グラフ構造を用いることで、この問題のようにデータ間の関係を視覚化して扱うことが可能になります。
- この問題は、「グラフ」構造で考えると「ある点から出発して全て線をちょうど一度ずつ通ることができるか?」という問題となります。このような線のたどり方を「オイラー路」といいます。
2018-秘密-解説
- 考案国:イタリア
- 正解
- 「3人のうち誰かが当たったと確信できるが、誰が当たったかは分からない」
- 説明
- 誰が当たったかを知ることなく、Xavier (X), Ylenia (Y), Zoe (Z) の誰かが当たったかどうかが知るのが目的です。
- 誰かが当たった場合は、その人は嘘をつきます。
誰かが嘘をつくことで、3人の証言に矛盾が生じるので、矛盾が置きているかどうか検証します。 - この問題では、『Xavier (X) は「同じ」と,Ylenia (Y) は「同じ」と,Zoe (X) は「異なる」と公表』しました。このように3人が公表した場合は、誰かが嘘をついたことを確認します。
- 1つ目の方法:
- 「X: 同じ、Y: 同じ、Z: 異なる」と3人とも正直に公表したと仮定します。
- X は「同じ」と言っていたので、X と Y のコイントスの結果と X と Z のコイントスの結果は同じになります。 Y は「同じ」と言っているので、X と Y のコイントスの結果と Y と Z のコイントスの結果は同じになります。したがって、3つのコイントスはすべて同じでなければなりません。つまり、「Z:異なる」という状況は生じません。これは、「3人とも正直に公表した」とする仮定と矛盾するので、誰かが「正直に公表した」のではない、誰かが宝くじに当たったと結論付けられます。
- 注意:この議論は、必ずしも Z が宝くじに当選したことを意味するものではありません。それは単に「3人とも正直に公表した」のは間違っていたということです。
- 2つ目の方法:
- 3つのコイントスの結果がどのようになるかの可能性は8通りあります。
全ての可能性それぞれに対して、3人とも正直に公表した場合はどのようになるか、真理値表を作ってみましょう。 - 最初の3つの列は、3つのコイントスの結果です。のこりの3つの列は、正直に公表した場合、Xavier (X), Ylenia (Y), Zoe (Z) が公表した内容です。
コイントス 公表内容 XY XZ YZ X Y Z 裏 裏 裏 同じ 同じ 同じ 裏 裏 表 同じ 異なる 異なる 裏 表 裏 異なる 同じ 異なる 裏 表 表 異なる 異なる 同じ 表 裏 裏 異なる 異なる 同じ 表 裏 表 異なる 同じ 異なる 表 表 裏 同じ 異なる 異なる 表 表 表 同じ 同じ 同じ - 「同じ、同じ、異なる」という行がないことがわかります。つまり、「同じ、同じ、異なる」と公表した場合は、誰かが嘘をついたことが分かります。
- 3つのコイントスの結果がどのようになるかの可能性は8通りあります。
- 実際のコンピュータでは
- この問題は、「食事する暗号学者の問題」として知られています。 これは、送信者と受信者の両方が追跡できない通信の例です。
- この問題に基づく匿名の通信ネットワークは、DCネットと呼ばれます(DCは「ダイニング暗号化 (Dining Cryptographers)」を意味します)。 個人データが同意なしに収集されることもある現在のインターネットでは、匿名性は重要な問題です。
- https://ja.wikipedia.org/wiki/食事する暗号学者の問題
(シニア問題に戻る)
 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は