シニア問題解説(高校２年生・３年生)

• A

  2013-回すオモチャ-解説

  • 正解は「ひだり→みぎ→みぎ→ひだり→みぎ→ひだり」
    • ビー玉を出すためには，下の図のような経路をたどる必要があります。
      
      そのためには，下の図のような順番で木の板を回せばよいのです。
      

  2013-観覧車-解説

  • 正解は「1,3,7,4」
    • まず，それぞれの名前から番号を計算します。
      Bill = 1 + 8 + 1 + 1 = 11 -> 1
      Zoe = 5 + 4 + 4 = 13 -> 3
      Lucy = 1 + 0 + 2 + 4 = 7 -> 7
      John = 9 + 4 + 7 + 3 = 23 -> 3
      ところが，Johnが乗り込む時，Zoeがすでに3に乗っているため，次の4に乗ることになります。

  2013-ビーバーショップ-解説

  • 正解は「C」
    • A 11/20(金)に4個の商品が売れた。
      • 売上ノートを見る限り、4個売れています
    • B 最初の2日間でいちばん売れた商品は「いちごチョコ」だった。
      • 一番売れているのは100番の商品＝いちごチョコ
    • C 最初の2日間で「ビーバー製菓」より「ビーバービバレッジ」のほうが多く売れた。
      • ビーバー製菓の100,102は5個
      • ビーバービバレッジの101,103,104,105も5個
      • 同じ
    • D 11/21(土)の売上は55ビブラだった。
      • 10*2+5*1+3*1+7*1+20*1=55
  • 解説
    • この問題は、リレーショナルデータベースの扱いと関連があります。
    • 商品ノートと売上ノートのうち、必要な列だけに注目したり、特定の条件に当てはまるデータを探したり、二つのノートの特定の列を結合させることは、リレーショナルデータベースでの基本操作です。

  2013-サイコロ-解説

  • 正解は「描画2, 回転90, 描画2, 描画3」
    • 描画2が取り得る形は
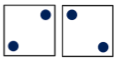
    • 描画3が取り得る形は
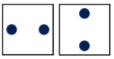
    • を作るには、描画2を90度回したものと、描画2と描画3をそのまま配置したもので実現可能
    • 描画2 -> 回転90 -> 描画2, 描画3
• B

  2013-ネックレス-解説

  • 正解は「32」
    • 最も短い長さを探します。
      
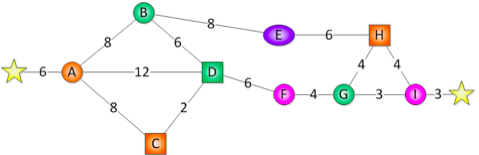
    • 考えられる最短の紐は、(A,B,E,H,I)か (A,C,D,F,G,I)
      • AD > ACDおよび GHI > GIのため、除外
    • (A,B,E,H,I)は 6+8+8+6+4+3 = 35
    • (A,C,D,F,G,I)は 6+8+2+6+4+3+3 = 32 <=最短

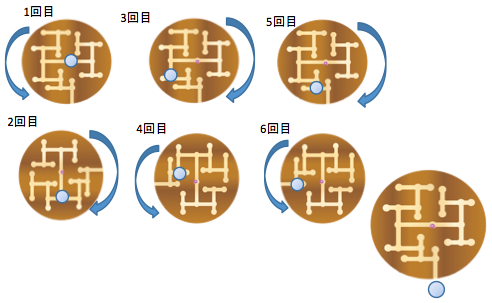
  2013-友だちの家-解説

  • 正解は「Yの家」
    • A,B,Cと下のように名付けます
      
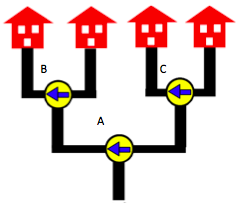
      Aは奇数では左、偶数では右なので、30日目は右
      Cは奇数回目で左、偶数回目で右になる
      30日目では15回目なので、左

  2013-川の点検-解説

  • 正解は「6匹」
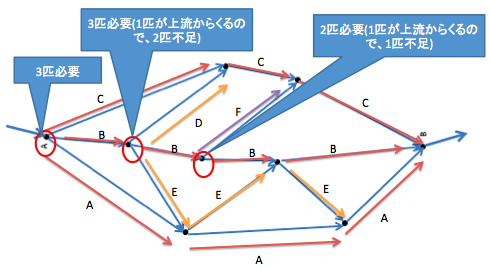
    • 下の図のように考えます
      

  2013-宝探し-解説

  • 正解は「225」
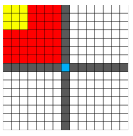
    • 1回で答えを得られるのは、3x3の正方形
      黄色を指定すると、その周囲のどれか確定可能です。
      
    • 2回で答えを得られるのは、7x7
      赤を指定すると、3x3に削減可能
      どの方向かがわかればそれ以外の方向は削除できます。
      同じ列、同じ行も削除可能（もしくはそのライン内になります。）
      
    • 3回で答えを得られるのは15x15
      青を指定すると7x7に削減可能
      よって225個の正方形であれば3回で宝にたどりつけます。
      
• C

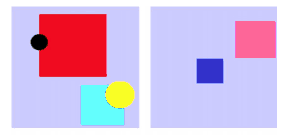
  2013-ランダムな絵-解説

  • 正解は
    
    
    
    • 問題の手順を整理すると次のようになります。
      • 円は同じ色のものしかない
      • 円の数と四角の数は同じ
      • 円を置いてから四角を置く（円は四角の後ろ）
        
    • この条件に合わないのは、
      
      しかし、○を四角の下に重なるように置くと右の図は実現可能
    • 左上のみ実現不可能

  2013-最短経路-解説

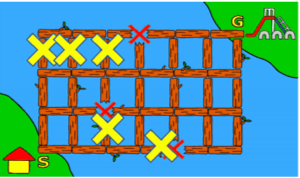
  • 正解は「18」通り

    

    • 黄色の×は通れません。
    • あるつなぎ目に右から至る経路も上から至る経路も戻ることになるので，最短経路ではありません。つまり，ある丸太のつなぎ目に至る最短経路数は，そのつなぎ目に左から至る最短経路数と右から至る最短経路数の和です。
    • そこで左下の角のスタート地点（ビ太郎の家(S)）から始めて，下の図のように今いるつなぎ目に至る経路数を右と上のつなぎ目に足していけば，右上の角のゴール（ビーバー公園(G)）に至る最短経路が 18 と分かります。

      

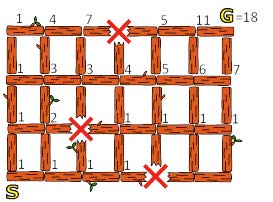
  • 解説
    • この解法は，動的計画法と呼ばれる手法の一例です。動的計画法では，部分問題を考え，容易に解ける小さな部分問題を先に解き，その答えを活用して解を求めていきます。
    • この場合の部分問題は，あるつなぎ目に至る最短経路数です。

  2013-古代火星語-解説

  • 正解は左下のメッセージです。

    

  • 4つの選択肢を眺めてみましょう。

    

  • 4つのメッセージは，7文字中連続した6文字が同一です．右下以外の3つのメッセージは，最後の1文字が異なるだけで1文字目から6文字目までは共通です。右下のメッセージの2文字目から7文字目までは，他の3つのメッセージの1文字目から6文字目までと共通です。

    

  • この共通する6文字に含まれる5つのパターン（隣合う2文字）から定まる点数は同じなので，残り1つのパターンの点を調べれば，実際にメッセージの点数を求めなくても最も点数が高いメッセージが分かります。
    • 左上の最後のパターンである「青青」は，最初に見つけた石のメッセージには現れません。つまり，0 をかけるので，点数は 0 になります。
    • 右上の最後のパターンと右下の最初のパターンは同じなので，右上と右下のメッセージの点数は同じです。
    • 左下の最後のパターンである「青赤」は，最初に見つけた石のメッセージに3回現れます．右上の最後のパターンと右下の最初のパターンである「青緑」は最初に見つけた石のメッセージに2回現れます。
  • つまり，4つの選択肢の中では，左下のメッセージの点数が最高です。
  • 解説
    この問題は，自然言語で書かれた文章をその内容を理解することなく解析するのに使われる言語モデルである n-グラムを題材にしています。このような言語モデルや言語認識や自動機械翻訳などの自然言語処理で用いられています。

  2013-森の木-解説

  • 正解は「A の木が 34 本，B の木が 55 本」
    • A は B を作り，その年で消える
    • B は A を作り，次の年に残る
      このことから，次がわかります。
    • A の本数は，前年の B の本数
    • B の本数は，前年の A の本数と B の本数の和
      • (前年の A の本数)+(前年 B の本数) = (前年の A の本数)+(今年の A の本数) = (前々年のBの本数+前年の B の本数)

  

  • 解説
    　この問題は，数列を再帰的な定義に関する問題で，数列中の数はそれ以前の数に基づき計算することで得られます．このような数列は，ただちに解を得るのは困難なため小さなサイズの問題から解かないとならない問題のアルゴリズムを設計する際に良く現れます．
    　この問題でも，すぐに10年後の木の本数を求められないので，1年後，2年後，3年後と順次求めます．このような手法は動的計画法 (dynamic programming) と呼ばれています．

（シニア問題に戻る）