JuniorAnswer2017
ジュニア問題解説(中学3年生・高校1年生)
- A
2017-泳いでどこに行く?-解説
- 考案国:スイス
- 正解
- 「(a)と(d)」
- 説明
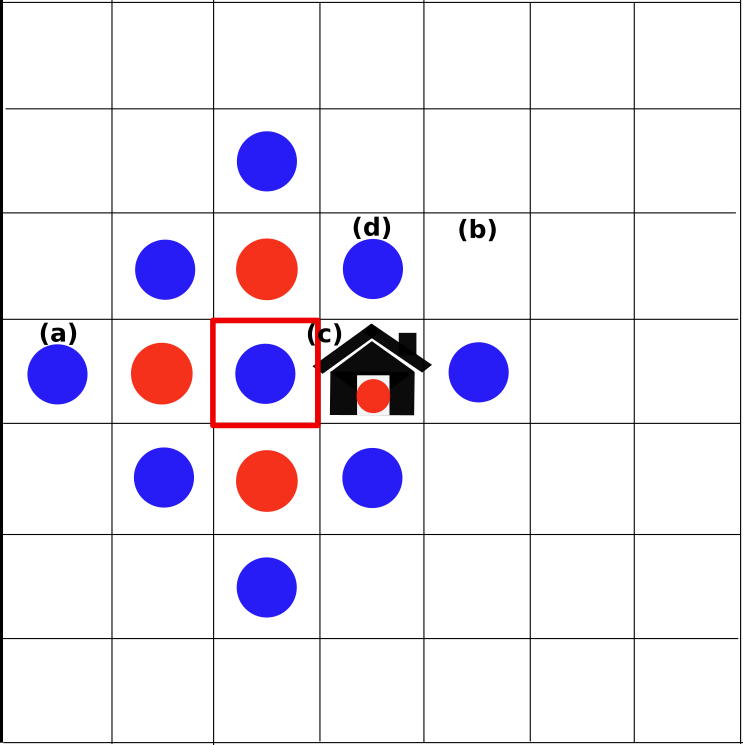
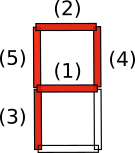
- マリアは3枚のカードを引きます。1枚目はダイヤだったので家の左に動きました(図の赤い枠の場所)。この状態で2枚目を引くと、図の赤い丸の場所に動けます。さらに3枚目を引くと、図の青い丸の場所に動けます。
- 実際のコンピュータでは
この問題では、ランダムな動きを扱っています。空気中の酸素や液体の拡散など、粒子の数が非常に多い動きのシミュレーションに使われます。
- マリアは3枚のカードを引きます。1枚目はダイヤだったので家の左に動きました(図の赤い枠の場所)。この状態で2枚目を引くと、図の赤い丸の場所に動けます。さらに3枚目を引くと、図の青い丸の場所に動けます。
2017-かぎかっこ-解説
- 考案国:オーストリア
- 正解
- 説明
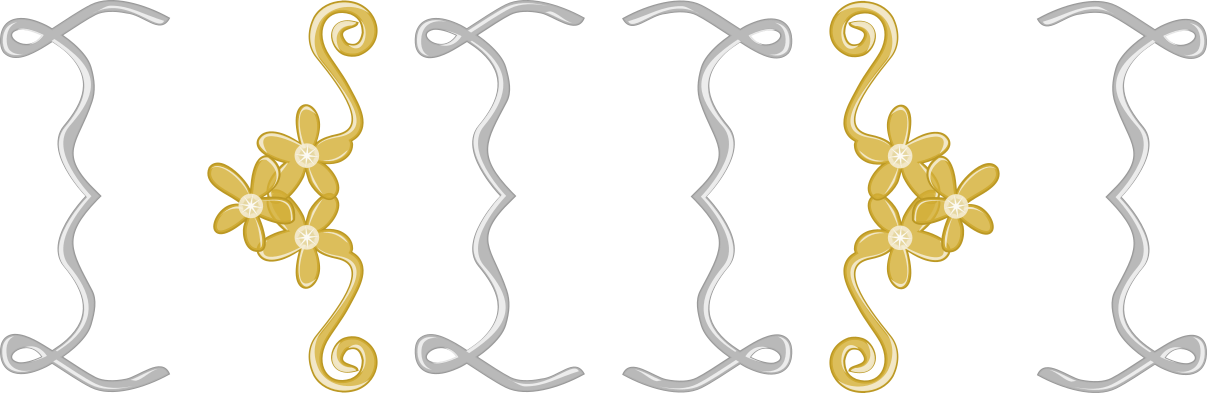
- 正解のブレスレットは、最初にペアを置き、その間にペアを置いて、さらにその間にペアを置いています。他のブレスレットは、規則に従っていません。
- 実際のコンピュータでは
ブレスレットの規則は、プログラムの文法を表しています。プログラムの中の"("と")"や、"{"と"}"は、ブレスレットと同様の規則でペアになって使われる必要があります。このような状態を「構文的に正しい」と言い、そうでない場合は構文エラーになってしまいます。
2017-ビーバートーナメント-解説
- 考案国:クロアチア
- 正解
- 説明
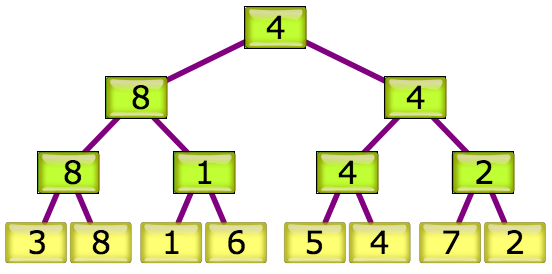
- いちばん下の最初の対戦で、勝った人の番号は混ざってしまったカードの中にあるはずです。
負けた人は、トーナメントの上位には現れません。なので、ゲームの結果を戻すには、最初のゲームの2人ずつのうち、どちらが残りのカードの中にあるかを調べればよいでしょう。 - 実際のコンピュータでは
注意深い観察と必要な条件を守ることは、適切な論理的な問題解決と異なるアルゴリズムの解法を構築するための基礎となります。条件が成り立つことを確認すること(ブランチ構造)に加えて、反復(繰り返し構造またはループ)は、一般的にコンピュータによる解法を設計する時に使われています。
- いちばん下の最初の対戦で、勝った人の番号は混ざってしまったカードの中にあるはずです。
2017-パン-解説
- 考案国:日本
- 正解
- 「フランスパンと食パン」
- 説明
- 正解は「フランスパンと食パン」です。
- 4つの条件に a 〜 d の番号をつけます。
- アリスとボブは同じ種類のパンを持っていません。
- チャーリーはフランスパンを持っています。
- ドローシーはメロンパンを持っていますが,アリスはメロンパンを持っていません。
- ボブはクロワッサンを持っています。
- これらの条件から分かることを、下のような表にまとめます。
アリス ボブ チャーリー ドローシー フランスパン Yes ( b ) メロンパン No ( c ) Yes ( c ) クロワッサン No ( a / d ) Yes ( d ) 食パン - アリスは、メロンパンもクロワッサンも持っていないことが分かったので、アリスが持っているのは「フランスパンと食パン」と分かります。
- 実際のコンピュータでは
数理論理学は数学的な証明を研究する学問で、ブール代数はその一部です。これは演繹論に基づいていて、真か偽という2種類の値を扱います。上の真理表はビーバーとパンの関係を表しています。
- 正解は「フランスパンと食パン」です。
- B
2017-おばあさんのジャム-解説
- 考案国:ロシア
- 正解
- 次の2種類の正解パターンがあります。
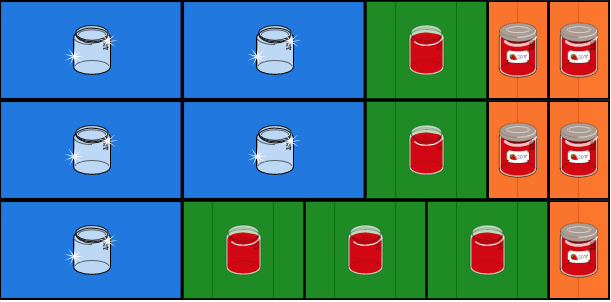
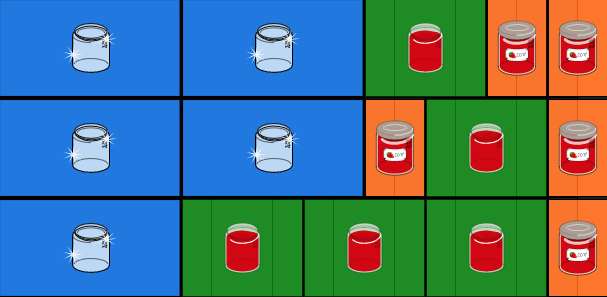
- 3人の役割は入れ替わっても良いので、上の正解パターンには3つの正解が、下の正解パターンには6つの正解が、つまり、合計で9つの正解があります。
- 次の2種類の正解パターンがあります。
- 説明
- 1個の瓶詰を作るには、3分と2分と1分で合計6分かかります。使える時間は3人で10分間の合計30分ですので、5個より多くは作れません。
そして、瓶を洗う前にジャムを入れることはできませんし、ジャムを入れる前に蓋をすることはできません。
- 1個の瓶詰を作るには、3分と2分と1分で合計6分かかります。使える時間は3人で10分間の合計30分ですので、5個より多くは作れません。
- 全員が次の方針で作業をすることを考えましょう。
- 洗った空(から)の瓶がないときは、瓶を洗う
- 洗った空の瓶があるときは、ジャムを入れる
- ジャムの入った蓋の開いた瓶があるときは、蓋をする
- この方針で作業すると、上の正解を作れます。
- 下の正解は、瓶を2個洗った2人うち一人が、瓶にジャムを入れる作業の前に蓋をした場合です。
瓶を2個洗い終わった時点では、ジャムが入った瓶は1つしかないので、瓶にジャムをいれる作業の前に蓋をできるのは1人だけです。
- 3人がうまく協調しないと、3人で10分間で5個の瓶詰を作れません。
- たとえば3人が独立して仕事をすると、次の図のように10分間で3個しか作れません。
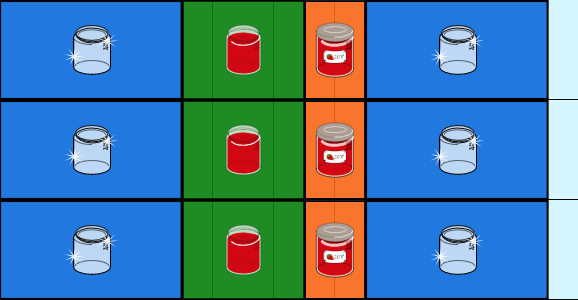
2人が担当する仕事を2種類ずつに減らしてしまうと、やはりうまく行きません。次の図のように、一番下の役割の人が2番目と3番目の蓋をする作業をしようとすると、まだジャムが入っていないので作業できず、10分間で3個しか作れません。
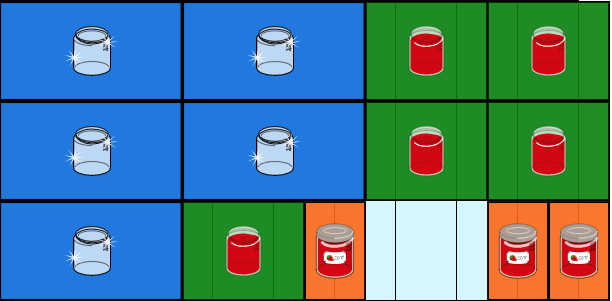
- たとえば3人が独立して仕事をすると、次の図のように10分間で3個しか作れません。
- 実際のコンピュータでは
この問題は、作業計画問題と作業の並列性を扱っています。
2017-新曲-解説
- 考案国:イラン
- 正解
- 「木曜日」
- 説明
- TomとTedとKimは1日目に、AnnaとJaneは2日目に、Joeは3日目に曲を買えます。
(火曜日の状態)
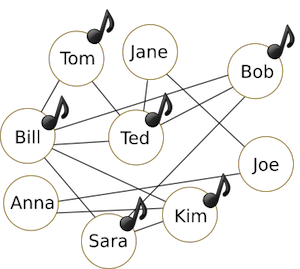
(水曜日の状態)
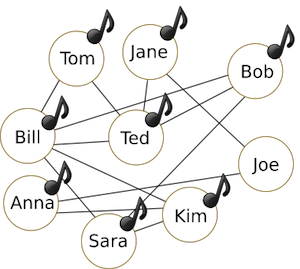
木曜日には、全員が曲を買いました。 - 実際のコンピュータでは
この問題は、SNSで影響が広がる様子を扱っています。ある情報が広がるかどうかは周りの友人たちのしきい値(ある一定の割合を超えているかどうか)に影響されます。このような研究はSNSにおける商品広告などで利用されています。
- TomとTedとKimは1日目に、AnnaとJaneは2日目に、Joeは3日目に曲を買えます。
2017-盾と矛-解説
- 考案国:日本
- 正解
- 説明
- 実際のコンピュータでは
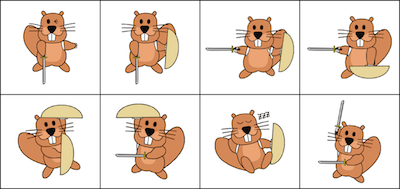
この問題は一見簡単そうに見えますが、実際にはとても複雑なパズルです。数枚の絵であっても、並べ方の組み合わせがあっという間に増えてしまいます。たとえば6枚の絵に1枚を加えて7枚にすると、6枚のときより6倍も組み合わせが増えてしまいます。式で書くとn枚のときは「(n-1)!」になり、7枚のときは「1×2×3×4×5×6」で720通りになってしまいます。(そして、ほとんどの組み合わせは不正解です)
バックトラックというアルゴリズムを使うとすべての組み合わせを調べることができますが、調べるための作業量が膨大になってしまいます。そこで、組み合わせを減らすように論理的に考えます。たとえば、剣を下に向けているビーバーは上の段にいるはずですし、盾の上にいるビーバーは1人だけです。
- 実際のコンピュータでは
2017-ファイル-解説
- 考案国:オーストリア
- 正解
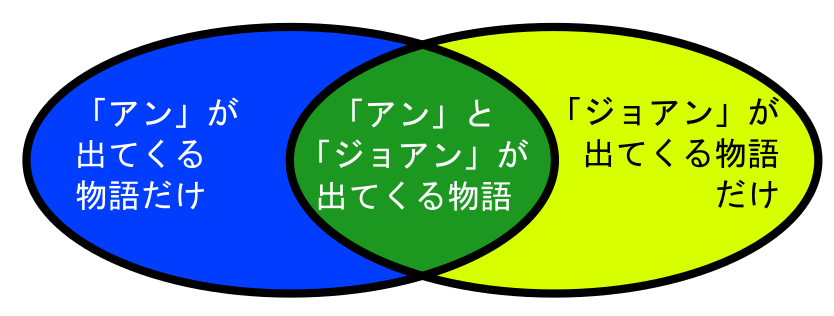
- 「「アン」が出て来る物語の一部も「アンの物語」のフォルダから消えてしまう。」
- 説明
- 最初に「アン」という文字が含まれるファイルをコピーしたときに、「アンの物語」のフォルダには、「アン」だけが含まれるファイル(図の青色)だけでなく、「アン」と「ジョアン」が両方とも含まれるファイル(図の緑色)が入った可能性があります。「ジョアン」が含まれるファイルを消すと、「ジョアン」だけが含まれるファイル(図の黄色)だけでなく、このようなファイル(図の緑色)も消されてしまうことになります。
- 実際のコンピュータでは
ファイルの検索は重要な作業です。ファイルは、ファイル名かファイルの中身で検索します。この問題のように、単純な操作でも誤ってファイルを消してしまうことがあります。機械的な操作だけに頼らずに、人の目でも確認しながら作業を行うことは有用です。
- 最初に「アン」という文字が含まれるファイルをコピーしたときに、「アンの物語」のフォルダには、「アン」だけが含まれるファイル(図の青色)だけでなく、「アン」と「ジョアン」が両方とも含まれるファイル(図の緑色)が入った可能性があります。「ジョアン」が含まれるファイルを消すと、「ジョアン」だけが含まれるファイル(図の黄色)だけでなく、このようなファイル(図の緑色)も消されてしまうことになります。
- C
2017-迷路脱出-解説
- 考案国:スイス
- 正解
- 説明
- 次の動きを2回繰り返すと出口に行くことができます。
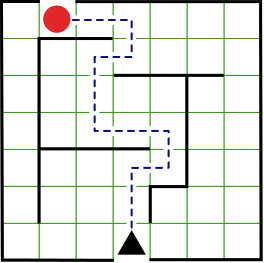
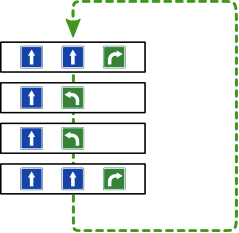
- 実際のコンピュータでは
プログラムは一連の命令で構成され、ときには一連の命令を繰り返す必要があります。これを簡単に可能にするために、プログラミング言語には「ループ」と呼ばれる特別な命令が提供されます。ループに入れられた命令は、開発者が決めた回数だけ繰り返すことが出来ます。
- 次の動きを2回繰り返すと出口に行くことができます。
2017-カラフルな建物-解説
- 考案国:日本
- 正解
- 説明
- アリスとボブとクリスが見える色を整理すると、次の表のようになりました。
ここから、次のことがわかります。その内容を下の図に表しました。
水 青 緑 オレンジ ピンク 赤 黒 黄 アリス ○ ○ ○ ボブ ○ ○ ○ クリス ○ ○ ○ あなた A C C 中央 A
・ボブは、アリスと同じ色(黒)を見ていて、クリスとも同じ色(赤)を見ています。よって、ボブはアリスとクリスの間(図の左上)にいることがわかります。
・アリスとクリスの場所はボブの隣であればよいので、アリスを右上、クリスを左下にしてみました。実際はアリスが左下、クリスが右上かもしれません。
・アリスから見えている色のうち、ボブとアリスが見ている色(黒)以外の色(水か黄)が、あなたからも見える色の候補です。(表のAの部分)
・クリスから見えている色のうち、ボブとクリスが見ている色(赤)以外の色(緑かオレンジ)が、あなたからも見える色の候補です。(表のCの部分)
・選択肢の候補から、「Aの色、ピンク、Cの色」または「Cの色、ピンク、Aの色」という並びを探してみましょう。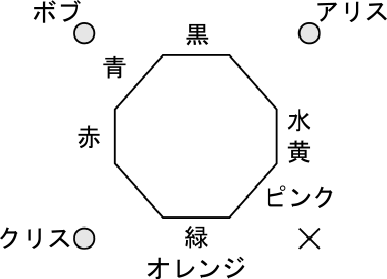
- アリスとボブとクリスが見える色を整理すると、次の表のようになりました。
2017-画像圧縮-解説
- 考案国:韓国
- 正解
- 「(111(1(1011)11))」
- 説明
- 全体を縦横半分ずつの4つの領域に分け、必要に応じてそれぞれの領域をさらに縦横半分ずつの4つの領域に分けて行きます。

- 実際のコンピュータでは
四分木は広い平面を簡潔に表現するために使われています。問題の例では、最初に全体を4つの領域に分けたときに、3つの領域(左上と右上と右下)を「111」というわずか3文字で簡潔に表現できています。また、画像全体を見ると、最初は画像を表すために64個の数字が必要でしたが、圧縮後は11個の数字と6個のカッコの記号の計17個の文字で画像を表現できています。
- 全体を縦横半分ずつの4つの領域に分け、必要に応じてそれぞれの領域をさらに縦横半分ずつの4つの領域に分けて行きます。
2017-数字の区別-解説
- 考案国:ロシア
- 正解
- 説明
- 4つの線分を使うと、 2x2x2x2 で 16 種類の形をつくれます。ですが、4つの線分だけでは、10種類の数字 (0 .. 9) を曖昧さなく区別することはできません。そして、正解は P の形だけになります。考え方を順に見ていきましょう。
- (1) 0 と 8 は、1つの線分が異なるだけです。そのため、0 と 8 を区別するには、この線分が必要です。
この線分を使っているかどうかで、0 から 9 の数字を {2, 3, 4, 5, 6, 8, 9} と {0, 1, 7} の2つのグループに分けます。 - (2) 1 と 7 も、1つの線分が異なるだけです。そのため、1 と 7 を区別するのは、この線分が必要です。
この線分を使っているかどうかで、{2, 3, 4, 5, 6, 8, 9} と {0, 1, 7} をそれぞれ2つのグループに、つまり、合計4つのグループに分けます: {2, 3, 5, 6, 8, 9}, {4}, {0, 7},{1}
1 と 4 は、1つだけのグループになったので、これらの2つの線分を使うだけで、1 と 4 は確認できます。 - (3) 他にも、1つの線分だけ異なる数字の組があります。8 と 9 です。8 と 9で異なる線分も必要です。同じように、この線分を使っているかどうかで、グループを分けると、{2, 6, 8}, {3, 5, 9}, {4}, {0}, {7}, {1} となります。
- (4) 6 と 8 も、1つの線分が異なるだけです。そのため、6 と 8 を区別するには、この線分が必要です。この線分を使っているかどうかで、グループを分けると、{2, 8}, {6}, {3, 9}, {5}, {4}, {0}, {7}, {1} となります。
- このように、4 つの線分だけでは、10種類の数字 (0 .. 9) を曖昧さなく区別できないことがわかります。
- (5) 3 と 9 も、 1つの線分が異なるだけです。この線分は、2 では使われていませんが、8 には使われているので、2 と 8 も区別できます。
- このように考えていくと、(1)から(5)の線分を使うことで、すべての数字を区別できることが表からわかり、正解の P の形が得られます。
線分 1 2 3 4 5 6 7 8 9 0 (1) o o o o o o o (2) o o o o o o o o (3) o o o o (4) o o o o o o o o (5) o o o o o o
- (1) 0 と 8 は、1つの線分が異なるだけです。そのため、0 と 8 を区別するには、この線分が必要です。
- 実際のコンピュータでは
パターン認識アルゴリズムは、一般に、統計的変動を考慮して、様々な入力に対して妥当な答えを提供したり、入力を「おおよそ近い」ものに対応させたりすることを意図しています。
パターン認識は、データ中のパターンや規則の抽出に焦点を当てた機械学習の一分野です。
認識手法の一つに、対象を一意に識別できる特徴を抽出するものがあります。
コンピュータビジョンは、現在、活発に発展している情報技術の一分野です。
- 4つの線分を使うと、 2x2x2x2 で 16 種類の形をつくれます。ですが、4つの線分だけでは、10種類の数字 (0 .. 9) を曖昧さなく区別することはできません。そして、正解は P の形だけになります。考え方を順に見ていきましょう。


 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は