CadetAnswer2021
カデット問題解説(中学1年生・2年生)
- A
2021-コインいれ-解説
- 考案国:アイルランド
- 正解

- 説明
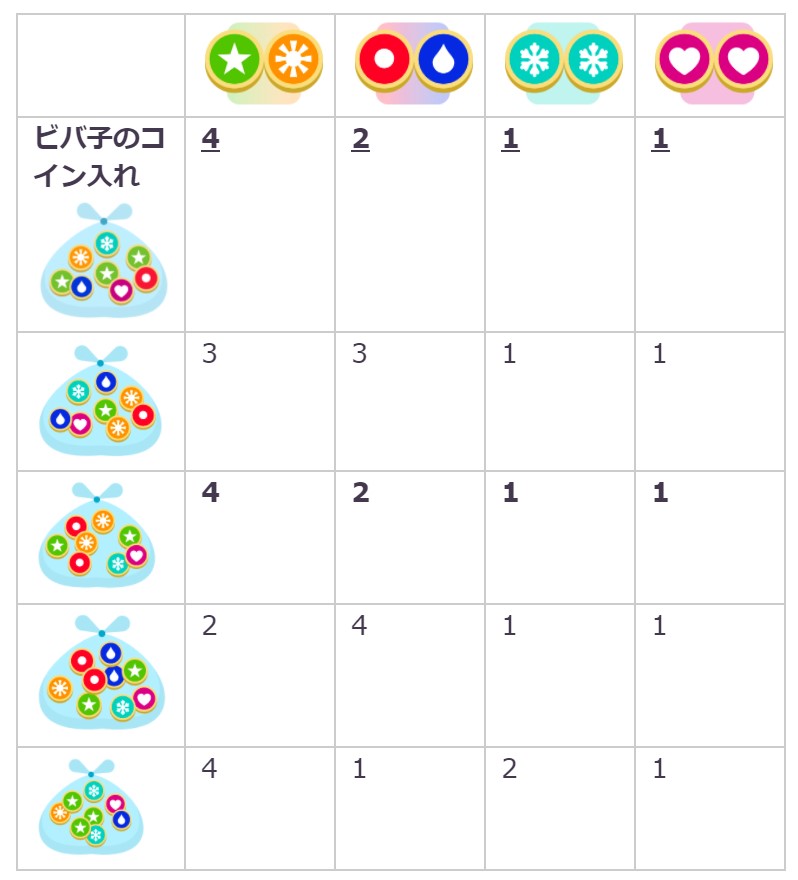
- ビバ子のコイン入れには、のコインが4枚、のコインが2枚、のコインが1枚、のコインが1枚、入っていました。
- 4つのコイン入れにどのコインが何枚ずつ入っているかを調べると、次の表のようになりました。ビバ子のコイン入れと同じコインが入ってるものを探しましょう。
- 実際のコンピュータでは
- この問題では、コインの表と裏を見ることで、「違うもののように見えるけれど、同じものを表している」データについて扱いました。
- たとえば、授業のアンケートで「楽しかった」「勉強になった」「受けてよかった」「またやってみたい」などは、表現は違いますが、同じ「よい授業だった」という情報を表しているかもしれません。
- コンピュータが日本語の文章などを解釈するときも、「楽しい」「嬉しい」「感動した」などを前向きな感情として近い意味として扱うことが行われています。
2021-カメ-解説
- 考案国:ドイツ
- 正解
- 説明
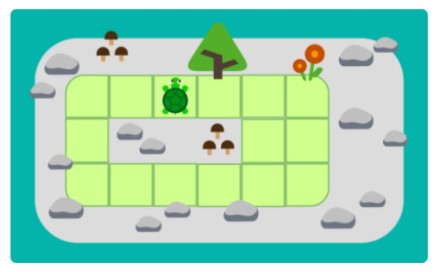
- それぞれの公園で、カメが草地を動く道を赤い線で描いてみました。
- 3つの公園では、カメはすべての草地を1回だけ歩くことができます。
- 左下にある公園は、すべてのマス目を1回だけ通ることができません。右にある6個のマス目は、上と下のどちらから歩いても、すべてのマス目を1回ずつ歩くことはできないのですね!
- 実際のコンピュータでは
- 草地を点と考えたとき、「すべての点を1回だけ通って歩く」問題や、「すべての点を1回だけ通って歩き、元の場所に戻る」問題は、以前から研究されてきました。
- すべての場合をコンピュータで試すことは可能ですが、効率よく正解を見つける方法は現在も研究が勧められています。
2021-ボール-解説
- 考案国:韓国
- 正解
- 次の図は、正解のひとつです。
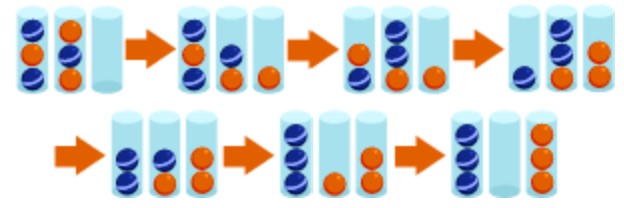
- 次の図は、正解のひとつです。
- 説明
- 別の移し方でも、同じ色のボールをすべて同じビンに入れることができます。
- 実際のコンピュータでは
- この問題では、ビンのいちばん上にボールを置いたり、いちばん上にあるボールを取り出したりすることができました。
- このように、「最後に入れたものを最初に取り出す」考え方をスタックと呼んでいます。スタックはコンピュータの中で、計算をするときなどに便利に使われています。
2021-せんろ-解説
- 考案国:ポルトガル
- 正解
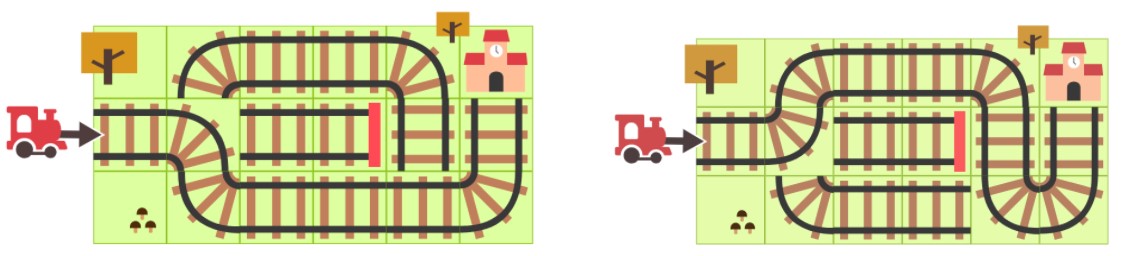
- 説明
- 2つの正解があります.
- 実際のコンピュータでは
- この問題では、列車を横や縦に進ませたり、左や右に曲げる線路を選びました。
- この問題のレールは、コンピュータのプログラムを表しています。
- 線路をうまく並べると、列車を正しい場所に進ませることができます。
- プログラムも同じように、命令をうまく並べると、コンピュータを正しく動かすことができます。
- みなさんが使う、スマートフォンやタブレット、パソコンなどのプログラムは、たくさんの命令を順番に実行しながら動いているのです。
- B
2021-ビーバーのおひゃくしょうさん-解説
- 考案国:トルコ
- 正解
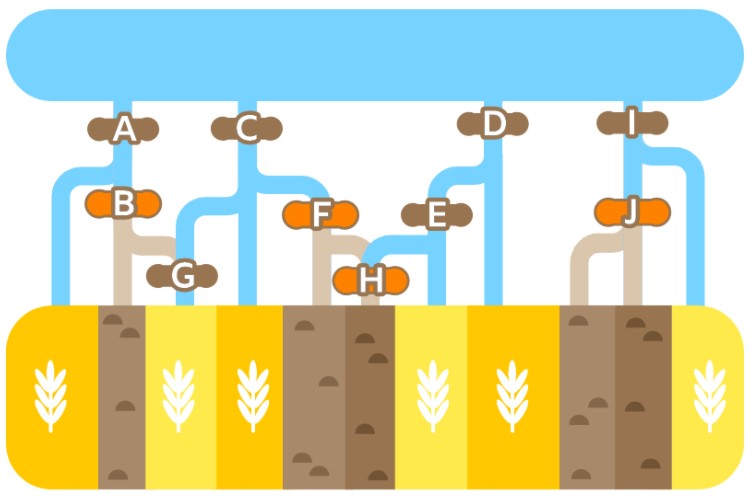
- 説明
- 茶色の畑には水が流れないように、せき止める場所を考えましょう。
- いちばん左の茶色の畑に水を流さないためには、Bで水を止める必要があります。
- 真ん中の2つの茶色の畑に水を流さないためには、FとHの両方で水を止める必要があります。
- 右の2つの茶色の畑に水を流さないためには、Jで水を止める必要があります。
- 実際のコンピュータでは
- この問題では、組み合わせを扱っています。
- たとえば、いちばん左の畑は「Aが開いている」ときに水が流れます。
- 左から2番目の茶色の畑は「AとBの両方が開いている」ときに水が流れます。
- 左から3番目のGの下にあるむぎの畑は「AとBとGがすべて開いている」ときか、「CとGの両方が開いている」ときに水が流れます。
- 「流れるか、流れないか」のような2種類の値を持つ条件を使い、それらを「両方開いている、どちらかが開いている」のように組み合わせて扱うことを、論理演算と呼び、プログラムの中で便利に利用されています。
2021-会えるかな?-解説
- 考案国:リトアニア
- 正解
- 2ひきのビーバーは、図のC5のはっぱで会えるかもしれません。
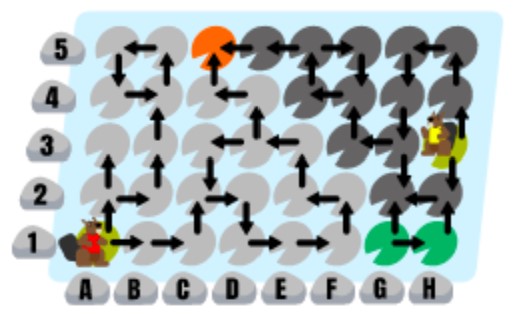
- 2ひきのビーバーは、図のC5のはっぱで会えるかもしれません。
- 説明
- 左下のビーバーは、スタートするときに、上と右のどちらに進むかを選べます。
- 上に行くとA3で行き止まりになるか、B4から始まるうずまきにはまってしまうかもしれません。
- スタートから右に行くと、D3まで進むことができます。
- D3では、左に進んで大きなうずまきを回るか、上に進んでもう一つの行き止まりであるC5に到達するかを選べます。
- 右にいるビーバーも、スタートするときに上と下を選べます。
- 下に行くと、G2で行き止まりになってしまいます。
- 上に行くとG3に進むことができます。
- G3では、下に行ってG2で行き止まりになるか、左に進んでE5まで進み、そこから右に進んでうずまきに入るか、左に進んでC5の行き止まりまで進むかを選べます。
- このように、C5のはっぱで2ひきのビーバーが会うことができることがわかりました。
- 左下のビーバーは、スタートするときに、上と右のどちらに進むかを選べます。
- 実際のコンピュータでは
- この問題では、スタートから出発して、分かれ道があるたびに、どちらに行くかを選ぶことができました。
- また、進んだ道が行き止まりになってしまったり、うずまきに入ってしまい進めなくなったときは、元の分かれ道に戻って、違う道に進むことができました。
- このように、いろいろな道を進んでみて、進めなくなったら少し戻って違う道を進む探し方をバックトラック(後戻り)と呼ばれ、コンピュータの中でデータを探すときなどに使われています。
2021-森の見はり-解説
- 考案国:オーストリア
- 正解
- 3つの見はり台を使った下の図が正解です。
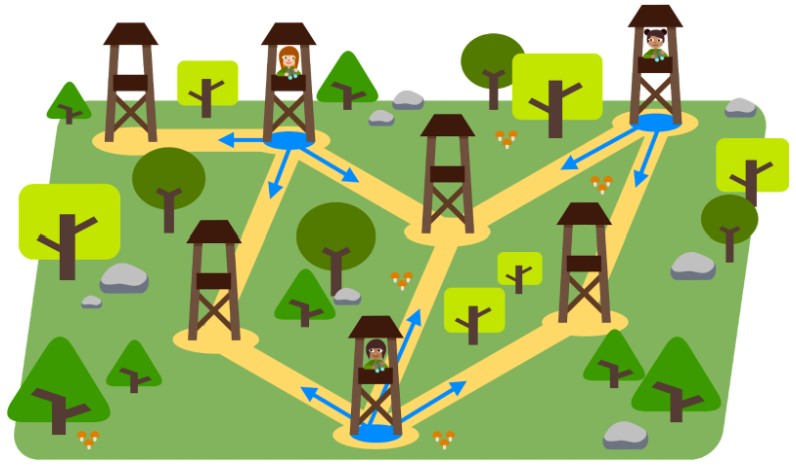
- 3つの見はり台を使った下の図が正解です。
- 説明
- 道は8本あります。
- もし見はりだいを2つしか使わないと、4本ずつ見はる必要がありますが、4本の道を見はることのできる見はりだいはありませんので、2つの見はりだいではぜんぶの道を見はれないことがわかります。
- 実際のコンピュータでは
- コンピュータの世界では、多くの情報を、点と線で表す「グラフ」で扱います。この問題では、グラフは次の図のように表せます。
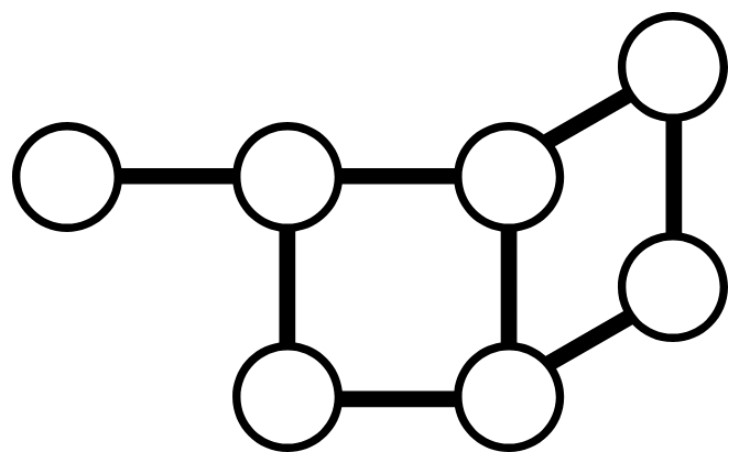
- この問題は、「すべての線が、選ばれた点のどれかにつながっている」と考えることができます。このような問題は最小頂点被覆問題と呼ばれ、「すべての通りを照らすことのできる街灯の配置」や「すべての廊下を撮影できるカメラの配置」などを考えるときに使うことができます。
- コンピュータの世界では、多くの情報を、点と線で表す「グラフ」で扱います。この問題では、グラフは次の図のように表せます。
2021-カッコウ-解説
- 考案国:カナダ
- 正解

- 説明
- 順に考えてみましょう。
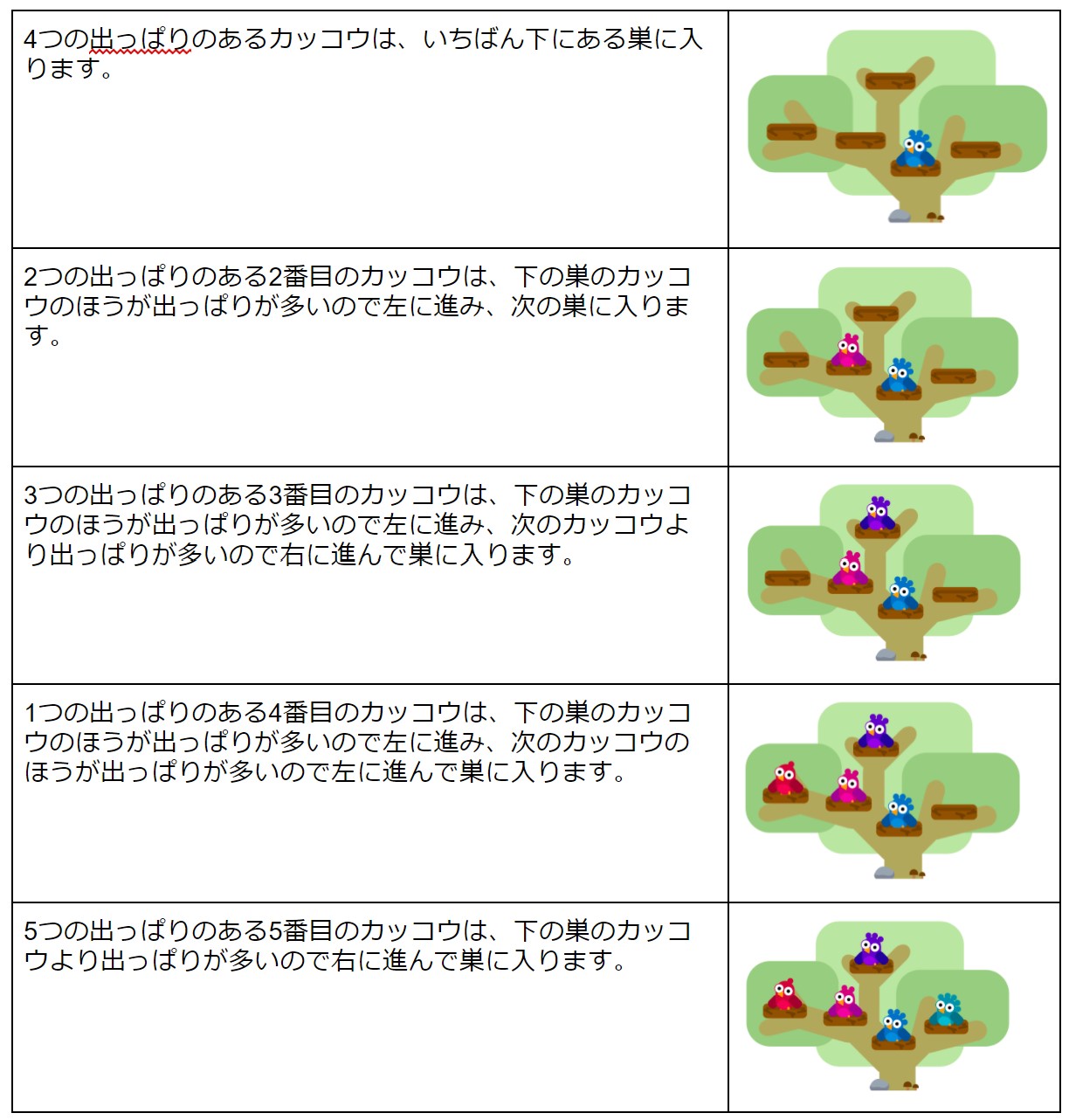
- 順に考えてみましょう。
- 実際のコンピュータでは
- この問題のように、データを木の形で表現することを、木構造のデータ構造と呼びます。
- データを木構造で表現し、値の大小を比較して適切な場所に入れて扱うと、「探している値が現在見ている値より小さければ左を探し、小さければ右を探す」のように、探す範囲を半分に絞りながらデータを高速に探すことができます。
- このような左右に分かれる木構造は二分木と呼ばれ、コンピュータのプログラムの中で、データを高速に検索する際に使われています。
- C
2021-いちご-解説
- 考案国:スイス
- 正解
- ビバ子はイチゴのかわりにきのこを置きました。そして、次の図のように枝を抜き取りました。
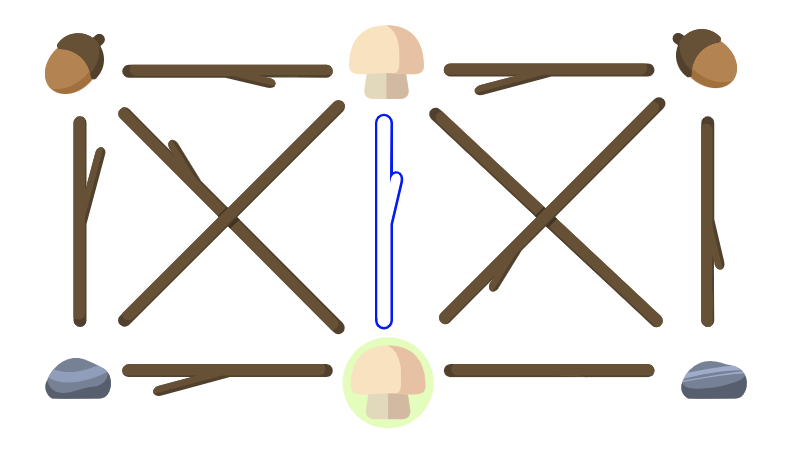
- ビバ子はイチゴのかわりにきのこを置きました。そして、次の図のように枝を抜き取りました。
- 説明
- イチゴが置かれていた「?」には、5本の棒が置かれています。
- どんぐりや小石を置くと、同じ種類の2箇所とつながっているため、2本の棒をぬき取る必要があります。
- きのこを置くと、きのことつながっている1本をぬき取るだけですみます。
- 実際のコンピュータでは
- ビ太郎が描いた絵は、点と線で関係を表す「グラフ」という構造で考えることができます。
- グラフの中で、「すべての点が、他の点とつながっている」ような点の集まりをクリークと呼びます。この問題の図では、左と右に、4個ずつの点から作られた四角形のクリークが2個あることがわかります。
- イチゴを他の物で置き換えると、置かれている物は3種類になりますので、4個の点を使ったクリークは作れなくなるはずです。そこで、4個の点から作られた2個のクリークを壊す棒を探すと、真ん中の縦の棒をぬき取ればよいことがわかります。
- この問題は、「最小限の色数でグラフを着色する問題」として知られています。そして、スポーツ競技のスケジュール管理、座席表の設計、数独の解答など、多くの用途で利用されています。
2021-枝がり-解説
- 考案国:ウズベキスタン
- 正解
- この図の赤色の枝を切り落とす 20 が正解です。
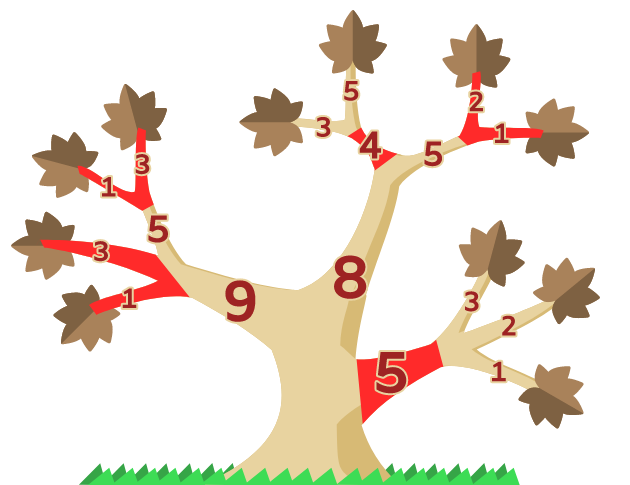
- この図の赤色の枝を切り落とす 20 が正解です。
- 説明
- 具体的に考えてみましょう。
- 左側の枝を考えると、葉が付いている細い枝を切ると「3+1」と「3+1」になります。「3+1」の代わりに5の枝を切ることもできますが、「3+1」のほうが4の時間で切れるので、5の枝を切るより短い時間で済むことがわかります。また、いちばん太い9の枝を切ることもできますが、細い枝を4本切ると「3+1+3+1」で8になるので、9の枝を切るより短い時間で済むことがわかります。
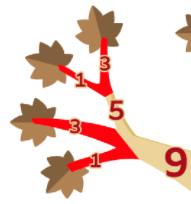
- 次に、上側の枝を考えると、左の2本を「3+5」で切るよりも、根本の4を切ったほうが短い時間で済むことがわかります。右の2本は「2+1」で3になりますので、根本の5を切るより短い時間で済むことがわかります。
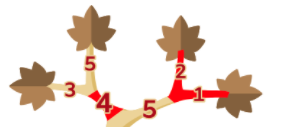
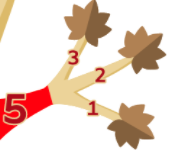
- 最後に右側の枝を考えると、3本を「3+2+1」で切るよりも、根本の5を切ったほうが短い時間で済むことがわかります。
- 実際のコンピュータでは
- 木構造はコンピュータ科学で重要なデータ構造です。
- 庭の木を木構造として考えることで、この問題は、根からすべての葉を分離するための、枝の最小の重みを求める問題として考えることができます。
- これはミニマルカット(略してmin-cut)と呼ばれるグラフ理論の標準的な問題で、様々な標準的なアルゴリズム(例えばFord-Fulkesronアルゴリズム)で解くことができます。
2021-プレゼント2-解説
- 考案国:ドイツ
- 正解
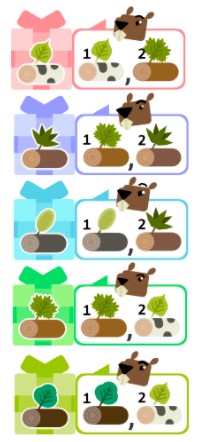
- 説明
- 同じプレゼントを欲しいビーバーが2匹いますので、全員に一番好きなプレゼントを渡すことはできません。まず、一番好きなプレゼントが重なっていない3匹については、そのプレゼントを渡すことにしましょう。
次に、一番好きなプレゼントが重なっている2匹について考えます。2匹を見ると、二番目に好きなプレゼントは、1匹はまだ渡されていませんが、もう1匹はすでに他のビーバーに渡されていることがわかります。
そこで、「2番目に好きなプレゼントが他のビーバーに渡されている」ビーバーに一番好きなプレゼントを渡し、「2番目に好きなプレゼントがまだ渡されていない」ビーバーに二番目に好きなプレゼントを渡すことで、すべてのビーバーが一番好きなプレゼントか二番目に好きなプレゼントを受け取ることができました。
- 同じプレゼントを欲しいビーバーが2匹いますので、全員に一番好きなプレゼントを渡すことはできません。まず、一番好きなプレゼントが重なっていない3匹については、そのプレゼントを渡すことにしましょう。
- 実際のコンピュータでは
- この問題では、ビーバーたちは一番目と二番目の希望を言いました。他のプレゼントは、すべて三番目と考えることができます。
- できるだけ一番目の希望をかなえるか、できるだけ二番目の希望をかなえる組み合わせが他にないとき、その組み合わせは最適になります。
- コンピュータ科学では、このような組み合わせ問題を「最大マッチング問題」と呼んでいます。組み合わせ問題にはいろいろなものがありますが、中には「安定した結婚問題」というものがあります。面白そうですよね。ぜひコンピュータ科学を学んでみてください!
2021-停電-解説
- 考案国:ハンガリー
- 正解
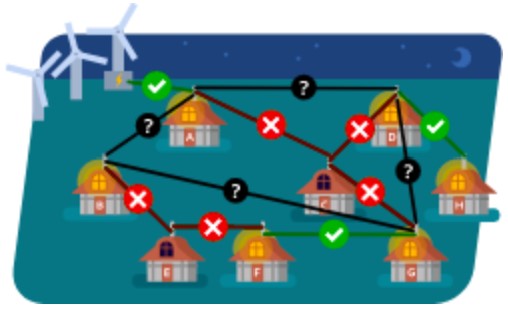
- 説明
- まず、停電している家を見ると、Eにつながる2本の電線と、Cにつながる3本の電線はすべて切れていることがわかります。1本でもつながっていれば、EやCは停電になりません。
- 次に、停電していない家を見ると、その家には電気が届いていることから、風車からAまでの電線は切れていません。Hにつながる電線も切れていません。Fにつながる電線は、Eとつながる電線は切れているので、Gとつながる電線は切れていません。
- 残りの停電していないB, G, Dの家は、複数の電線でAとつながっています。そのため、たとえばBの家は、Aとつながる電線が切れても、Gとつながる電線から電気をもらえます。このように、A,B,G,D,Aをつなぐ電線は、どれか1本が切れても停電しないことがわかります。
- 実際のコンピュータでは
- コンピュータのネットワークでは、この問題の電線と同様に、多くの通信線で実現されています。通信線の中には、速度が遅かったり、過負荷だったり、あるいは完全に壊れていたりといったような、障害が発生することがあります。ネットワークの構造に冗長性を持たせることで、1箇所で障害が発生しても継続的に利用できるようになる工夫が行われています。
- コンピュータの科学者は、ネットワーク構造を表現するために、「グラフ」という表記法を使います。グラフを扱うアルゴリズムは数多く存在します。例えば、ネットワーク構造を考えた上で、できるだけ効率的に障害のある線を発見することができます。
- システムの故障(エラー)を修正することは、コンピュータネットワークだけでなく、ソフトウェア開発においても、コンピュータ科学者が頻繁に行う作業です。エラーを修正するためには、その原因を正確に特定する必要があり、この作業は通常、いくつかのステップで徐々に行われます。プログラマーの中には、プログラムに含まれるすべてのエラーやバグを見つけることはできないと考える人もいます。
 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は