CadetAnswer2019
カデット問題解説(中学1年生・2年生)
- A
2019-飾りつけ-解説
- 考案国:ハンガリー
- 正解
- 説明
- 正解はBです。
Bでは、テーブルクロスの色が毎回変わり、3種類の花がすべて使われています。
AとDでは、テーブルクロスの色が隣と同じものがあります。
Cでは、2種類の花が使われていて、1種類でも3種類でもありません。
- 正解はBです。
- 実際のコンピュータでは
- コンピュータでは、複数の条件を満たしているかどうかを調べる論理演算は重要です。ANDは2つの条件を満たしているかを調べる論理積です。ORは少なくともどちらかの条件を満たしているかを調べる論理和です。
この問題では、「1種類の花か3種類の花が使われている」という論理和(OR)と、「テーブルクロスが交互に並べられていて、1種類か3種類の花が使われている」という論理積(AND)が組み合わされて使われていました。
このような問題を解くことで、論理的思考を向上させることができます。
- コンピュータでは、複数の条件を満たしているかどうかを調べる論理演算は重要です。ANDは2つの条件を満たしているかを調べる論理積です。ORは少なくともどちらかの条件を満たしているかを調べる論理和です。
2019-ビーバーコイン-解説
- 考案国:スイス
- 正解
- 説明
- 最適な解は「8ビーロが1枚、4ビーロが1枚、1ビーロが1枚」です。
16ビーロでは大きすぎます。8ビーロを使うと残りは5ビーロで、いちばん近いのは4ビーロです。そうすると残りは1ビーロで、2ビーロだと大きすぎるので1ビーロを使います。
- 最適な解は「8ビーロが1枚、4ビーロが1枚、1ビーロが1枚」です。
- 実際のコンピュータでは
- コンピュータではさまざまな種類のデータを扱います。この問題では数を表す数値データを扱いました。
数値を表すときは、13の例だと「8を1枚、4を1枚、1を1枚」のほかに、「4を3枚、1を1枚」や「4を2枚、2を2枚、1を1枚」「1を13枚」などさまざまな表現ができてしまいます。
これでは表現があいまいになってしまうため、「最も少ない枚数のコインで表す」というルールを加えることで、「8を1枚、4を1枚、1を1枚」という最適な表現に決まるようにしています。
- コンピュータではさまざまな種類のデータを扱います。この問題では数を表す数値データを扱いました。
2019-買い物するビ太郎-解説
- 考案国:日本
- 正解
- 「6番目に高い」
- 説明
- ビ太郎が持っているお金で払える額を高い順に並べると次のようになり、「11010」は6番目に高いことがわかります。
1番: ฿11111
2番: ฿11110
3番: ฿11101
4番: ฿11100
5番: ฿11011
6番: ฿11010
7番: ฿11001
…
- ビ太郎が持っているお金で払える額を高い順に並べると次のようになり、「11010」は6番目に高いことがわかります。
- 実際のコンピュータでは
- この問題では、ビ太郎は1種類のお金を1個ずつしか持っていないので、金額を「その種類のお金を持っているか、いないか」という1か0で表すことができました。
- これはコンピュータが計算で使う2進数と似ています。2進数では0と1だけを使って数を表現します。この例の5桁の2進数では32通りの数を表現できます。
2019-お皿-解説
- 考案国:ロシア
- 正解
- 「3回」
- 説明
- この問題では、3枚のお皿を移動する必要があります。大きな皿の4枚目を入れるには中くらいの皿を1枚動かす必要があり、そのためには小さな皿を1枚動かす必要があるからです。
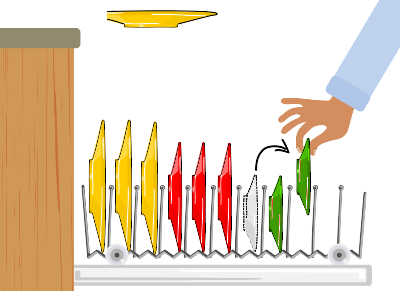
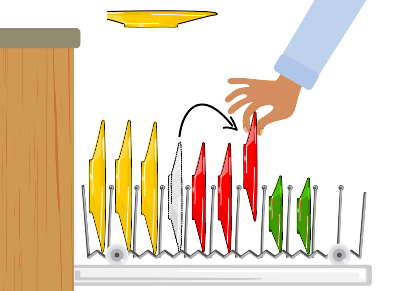
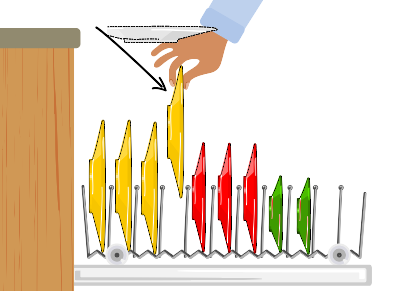
- この問題では、3枚のお皿を移動する必要があります。大きな皿の4枚目を入れるには中くらいの皿を1枚動かす必要があり、そのためには小さな皿を1枚動かす必要があるからです。
- 実際のコンピュータでは
- 大きさの順に並んでいるデータの中に新しいデータを加えるときは、コンピュータもこの問題と同じようにデータを扱います。
- コンピュータの処理は高速ですが、コンピュータが扱うデータの数が数億個のように多いときには、すべてのデータを1個ずつずらす処理はさすがのコンピュータでも時間がかかってしまいます。
- そこでコンピュータ科学者は知恵を絞って効率のよい工夫を考えます。全部で100万枚のお皿がある場合でも、今回の問題のようにお皿の種類が3種類しかない場合には、たった3枚のお皿を動かすだけで新しいお皿を適切な場所に入れることができるのです。
- B
2019-二重駐車-解説
- 考案国:ドイツ
- 正解
- 「Iの車」
- 説明
- Iの車を出すためには、Nの車を動かす必要があります。そのためには、左と右のどちらの方向にもOとMの車があるため、最初にOかMの車を動かしてから、次にNの車を動かす必要があります。
- 実際のコンピュータでは
- この問題を考えるときに、コンピュータはすべての車について、可能性をひとつひとつ調べていくかもしれません。このような「しらみつぶし」の調べ方はブルートフォース(総当り検索)と呼ばれます。
- 車の効率のよい駐車方法は多くの研究が行われています。駐車中の車を自動的に最適な場所に移動させるシステムも研究されています。
2019-キープ-解説
- 考案国:日本
- 正解
- 「3本」
- 説明
- 1本のキープでは、0,1,2,3の4通りを表せます。2本のキープでは、4通り×4通りで16通りを表せます。3本のキープでは、4通り×4通り×4通りで64通りを表せますので、50種類を表すことができます。
- 実際のコンピュータでは
- 私たちは生活の中で、「1つの桁で10通りの数を表す」10進法で数を扱っています。これは「結び目が0個から9個あるキープ」に相当します。10進法では、1本のキープで0から9までの10通りの数を表し、2本のキープで10通り×10通りで0から99までの100通りの数を表します。
- コンピュータは「1つの桁で2通りの数を表す」2進法で数を扱っています。これは「結び目が0個か1個のキープ」に相当します。
2019-梱包マシン-解説
- 考案国:日本
- 正解
- 「ブロックL」
- 説明
- 梱包マシンは次のように動きます。
1.「3, 1, 1」のボタンで、下から「L, C, D」の順にブロックが置かれます。
2.「4, 4」のボタンで「D, C」が順に取り除かれ、「L」が残ります。
3.「2, 3」のボタンで「I, O」の順にブロックが置かれ、下から「L, I, O」になります。
4.「4」のボタンで「O」が取り除かれ、下から「L, I」になります。このとき、上から2番目のブロックは「L」です。
- 梱包マシンは次のように動きます。
- 実際のコンピュータでは
- この機械では、最後に置かれたブロックが最初に取り除かれます。このようなデータ構造をスタックと呼びます。
- スタックはコンピュータのプログラムでよく使われます。たとえば「1+(2*(3+4)+5)」のような文字列の中で開き括弧「(」と閉じ括弧「)」の数が同じかどうかを確かめるときに利用されます。
2019-ボトルリサイクル-解説
- 考案国:ルーマニア
- 正解
- 説明
- 正解は2です。
選択肢ごとに図を描いてみるとわかりやすいです。図で、白色はwhite、緑色はcolorです。
図1
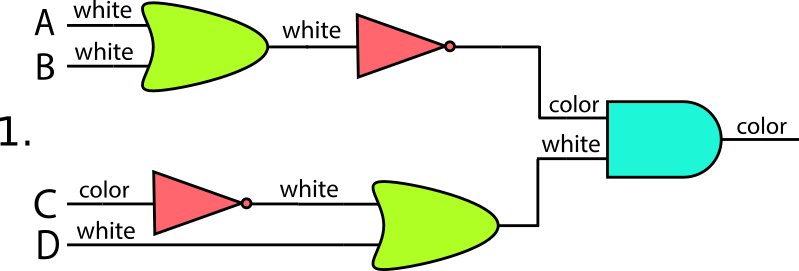
図2
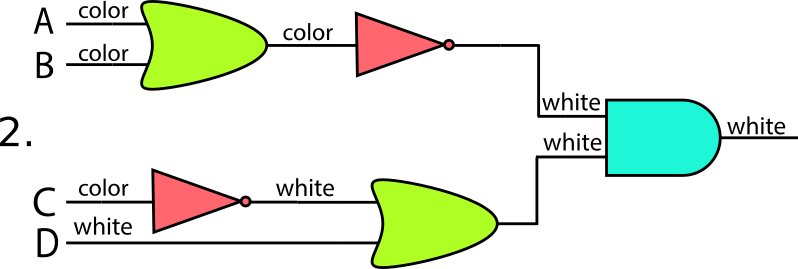
図3
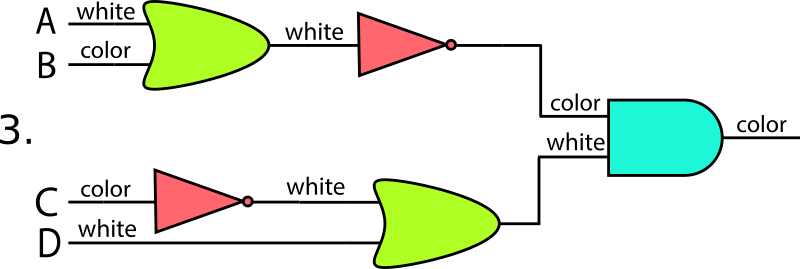
図4
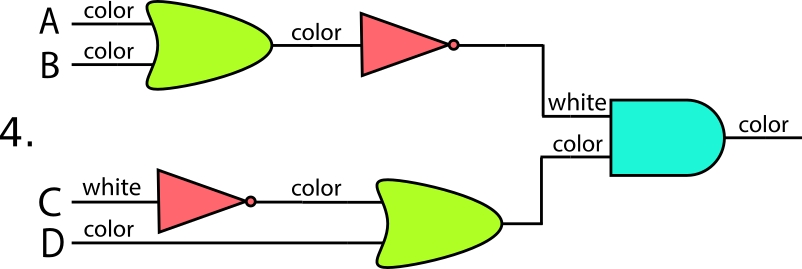
- 正解は2です。
- 白色のボトルを生産するには、次の3種類の入力が考えられます。
A color color color B color color color C color color white D color white white 正解の2
- 実際のコンピュータでは
- コンピュータのCPUは論理回路と呼ばれる微小な電子回路から作られています。論理回路ではNOT, OR, AND, XORなどが使われます。この問題ではAND, OR, NOTを使いました。説明図では実際の電子回路と同じ図で表しています。
- 実際の論理回路では、電気信号の有無で1と0を表します。これは論理回路の真と偽を表しています。この問題では白色(white)を真(1)、緑色(color)を偽(0)の役割で考えました。
- ANDでは両方の入力が真のときに出力が真になります。

- ORでは少なくともどちらかの入力が真のときに出力が真になります。

- NOTでは入力と出力が逆になります。入力が真のときは出力が偽になり、入力が偽のときは出力が真になります。

- ANDでは両方の入力が真のときに出力が真になります。
- C
2019-スカーフ制作機-解説
- 考案国:リトアニア
- 正解
- 説明
- 正解はAです。
図の上の中央にある草は続けて現れることができますが、図の下の中央にある木の枝は繰り返すことができないことに注意しましょう。また、図の出口の青い花から、入口の紫の花に戻ることはできません。
- 正解はAです。
- 実際のコンピュータでは
- この問題のように、入口から矢印をたどりながら「今どこにいて、次はどこに移る」を繰り返して出口に行けるかを表す図をオートマトンまたは状態遷移図と呼びます。
- オートマトンは、プログラムが文法通りに書かれていることを確認したり、PCやスマートフォンで入力された文字を日本語に変換する処理、電卓で数式が正しいことを確認する処理などで利用されています。
- たとえば、多くの電卓では「12+3=」を入力すると正しく計算が行われますが、「12++3=」はエラーになって計算されません。これは電卓の中に「数字の繰り返しと、演算記号と、数字の繰り返しと、最後に=」を表すオートマトンが定義されているため、正しい数式かどうかをチェックできているのです。
2019-トンネル-解説
- 考案国:タイ
- 正解
- 「BBGBGG」または「BBBGGG」
- 説明
- 出口でいちばん左が青(B)になるためには、入口の左がBBであることが必要です。そうでないと出口でいちばん左が緑(G)になってしまいます。
出口でいちばん右が緑(G)になるためには、入口の右がGGであることが必要です。そうでないと出口でいちばん右が青(B)になってしまいます。
そうすると、入力の真ん中の2つはBGかGBになります。どちらの場合も出力の真ん中の2つはBGになるため、両方とも正解であることがわかります。
- 出口でいちばん左が青(B)になるためには、入口の左がBBであることが必要です。そうでないと出口でいちばん左が緑(G)になってしまいます。
- 実際のコンピュータでは
- インターネットの通信で、パケットと呼ばれるデータはIP通信のルールで相手に送られます。ネットワークは「学校内のネットワーク」のように他のネットワークと分かれていて、お互いに直接通信できません。そこでルーターと呼ばれる中継装置を置くことで、適切な経路でパケットを送るようにしています。
2019-倉庫-解説
- 考案国:ロシア
- 正解
- 「10」
- 説明
- 1, 2, 3, 4, 5番のハリネズミと31, 32, 33, 34, 35番のハリネズミは荷物を移動しなくてすみます。
まず、問題の例にあるように、1番のハリネズミは荷物を移動しなくてすみます。実は1番だけでなく、2番から5番のハリネズミも同じです。
次に倉庫の数(5個と6個)を考えると、5で割っても6で割っても余りが0になる数は、0の次は最小公倍数の30です。
そこで、「0に続く1, 2, 3, 4, 5」の次は、「30に続く31, 32, 33, 34, 35」であることがわかります。
- 1, 2, 3, 4, 5番のハリネズミと31, 32, 33, 34, 35番のハリネズミは荷物を移動しなくてすみます。
- 実際のコンピュータでは
- この問題では、データを分割して格納する考え方を扱いました。ハッシュ法と呼ばれるアルゴリズムでは、データを複数の入れ物(倉庫)に分割して格納し、取り出すときは値からどの入れ物に入っているかを計算で求めることで、高速にデータを取り出します。
- わかりやすい例だと、生徒の名簿をアルファベットごとの入れ物に分けておき、「MattiaさんはMの入れ物に入れる」ようなイメージです。
- 今回の問題では、どの入れ物に入っているかを、剰余(割り算の余り)で求めました。例えば倉庫が5個のとき、「1番の倉庫は、1や6のように5で割ったときの余りが1の荷物を入れる」「2番の倉庫は、2や7のように5で割ったときの余りが2の荷物を入れる」「5番の倉庫は、5や10のように5で割ったときの余りが0の荷物を入れる」というやり方です。このようにすると、「13番の荷物はどこにあるかな?」と考えたときに、「13を5で割った余りは3だから3番の倉庫!」とすぐにわかります。
2019-3つの数字で描け-解説
- 考案国:スロバキア
- 正解
- 説明
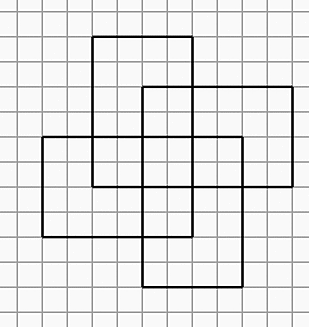
- 実際に、紙に描いてみるとわかりやすいと思います。「1, 4, 1」の場合はこのようになります。
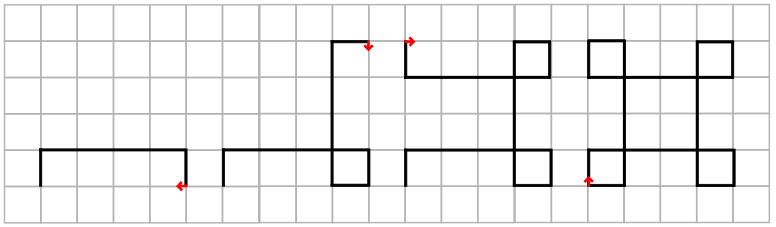
- 実際に、紙に描いてみるとわかりやすいと思います。「1, 4, 1」の場合はこのようになります。
- 実際のコンピュータでは
- コンピュータは与えられたプログラムで動きます。プログラムの命令はひとつひとつが意味を持っていて、コンピュータはそれを順番どおりに実行します。
- この問題では、コンピュータになったつもりで、与えられた命令を実行しました。命令を読んで、ひとつひとつがどのような結果になるかを考えることは、プログラムを作るときと、プログラムを修正するときに重要なスキルです。





 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は