シニア問題/C最短経路
最短経路
ビ太郎はビーバー公園で遊ぶのが大好きです。ビ太郎の家(S)とビーバー公園(G)は,次の図のように同じ長さの丸太で作られた橋でつながっています。X印の丸太の繋ぎ目は,壊れていて通れません。
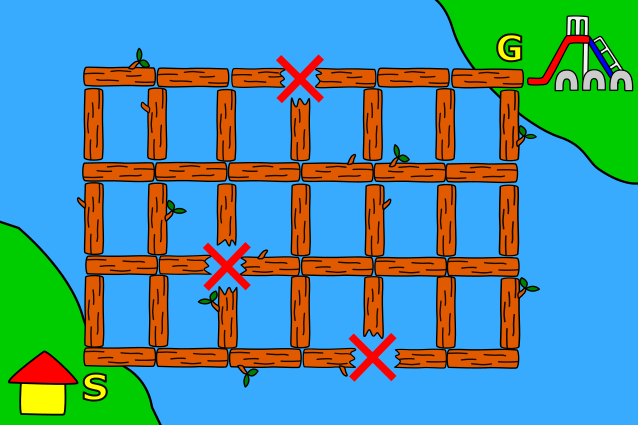
ビ太郎の家からビーバー公園までの最短経路(最低限の本数の丸太で行ける道すじ)は何通りあるでしょう?
- 解説を見る
- 正解は「18」通り
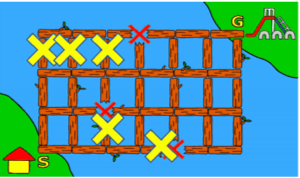
- 黄色の×は通れません。
- あるつなぎ目に右から至る経路も上から至る経路も戻ることになるので,最短経路ではありません。つまり,ある丸太のつなぎ目に至る最短経路数は,そのつなぎ目に左から至る最短経路数と右から至る最短経路数の和です。
- そこで左下の角のスタート地点(ビ太郎の家(S))から始めて,下の図のように今いるつなぎ目に至る経路数を右と上のつなぎ目に足していけば,右上の角のゴール(ビーバー公園(G))に至る最短経路が 18 と分かります。
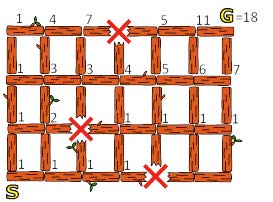
- 解説
- この解法は,動的計画法と呼ばれる手法の一例です。動的計画法では,部分問題を考え,容易に解ける小さな部分問題を先に解き,その答えを活用して解を求めていきます。
- この場合の部分問題は,あるつなぎ目に至る最短経路数です。
- 正解は「18」通り


 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は