2020-線をつなごう-解説
- 考案国：マケドニア
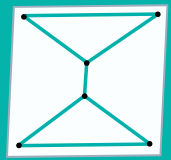
- 正解
- 説明
- それぞれの点に、何本の線がつながっているかを数えてみましょう。つながる線の数が2本や4本のような偶数（2で割り切れる数）か、1本や3本のように奇数（2で割り切れない数）かが重要です。
- 点につながる線の数が、「すべての点で偶数」か「2個の点だけ奇数」の絵は一筆書きで描けます。正解の絵は、真ん中の2つの点につながる線が、それぞれ3本と3本で、「2個の点だけ奇数」になりますので、一筆書きでえがけることがわかります。
- （理由）
- 一筆書きで線をえがくときに、途中で通る点は、「その点に入る線と、その点から出ていく線」がありますので、途中の点につながる線は2本や4本などの偶数になるはずです。
- つぎに、一筆書きの「はじめの点」と「終わりの点」を考えると、「はじめの点と終わりの点が同じ」ときはその点につながる線は2本などの偶数になりますが、「はじめの点と終わりの点が別」のときはそれぞれの点につながる線は1本や3本などの奇数（2で割り切れない数）になります。
- よって、点につながる線の数が、「すべての偶数」か「2個の点だけ奇数」の絵は一筆書きで描けることがわかります。
- 実際のコンピュータでは
- この問題では、描いた絵を「グラフ構造」で表しています。グラフ構造の「点と線」のようなシンプルな形で表すことで、問題をコンピュータを用いて解くことができるようになります。
注があるものを除き, このサイトの内容物は
