2019-秘宝の地図-解説
- 考案国：ベトナム
- 正解
- 説明
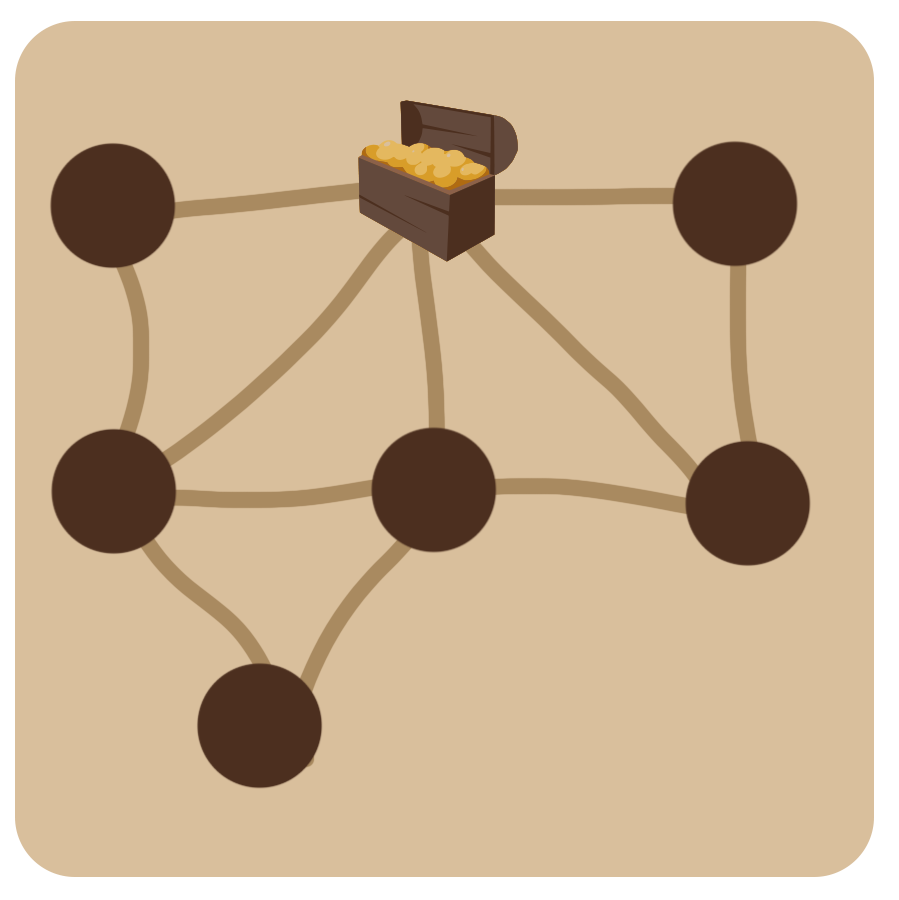
- 地図には7個の区域があります。そこで、宝を含めて丸（●）が6個しかないものは正解ではありません。
- 次に、それぞれの区域が何個の区域と隣り合っているかを数えます。宝のある区域は5個の区域と隣り合っています。そこで、宝から4本しか線が出ていないものは正解ではありません。
- 残りの2つのどちらが正解かを調べるために、区域にaからgまでの名前を付けて、それらが何個の区域と隣り合っているかを数えてみましょう。
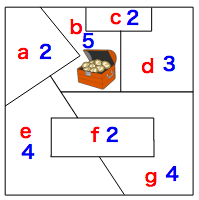
区域aは、b, eの2個と隣接しています。
区域bは、a, c, d, e, gの5個と隣接しています。
区域cは、b, dの2個と隣接しています。
区域dは、b, c, gの3個と隣接しています。
区域eは、a, b, f, gの4個と隣接しています。
区域fは、e, gの2個と隣接しています。
区域gは、b, d, e, fの4個と隣接しています。
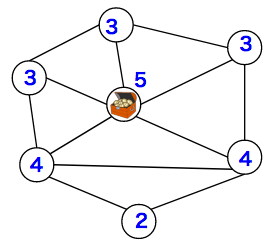
隣接している数を見ると、「5個が1区域、4個が2区域、3個が1区域、2個が3区域」あることがわかります。 - 正解でないほうの選択肢を描くと、このようになりました。3個の区域が3個ありますので、正解でないことがわかります。
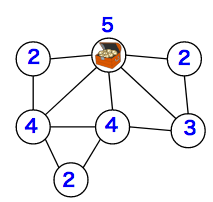
- もうひとつの選択肢を描くとこのようになりました。「5個が1区域、4個が2区域、3個が1区域、2個が3区域」あることがわかります。
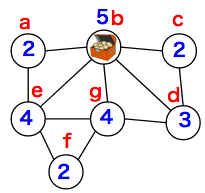
念のために、図に区域を書き込んで確かめることができます。
- 実際のコンピュータでは
- この問題では、点（頂点）と線（辺）で表される「グラフ構造」が実際の問題を解くときに有効なことを学びました。頂点は区域を表し、辺は「区域が隣り合っている」という関係を表しています。
- グラフ構造は、複数のものごとの関係を表すときに便利です。数学者とコンピュータ科学者は、グラフ構造を使うことで、現実の問題を解決するためのたくさんの有用なアルゴリズムを考えてきました。
注があるものを除き, このサイトの内容物は
