2014-カッコを使わない数式-解説
- 正解は「2 a b × a c × b c × + + ×」です。
- 正解の式はこのように通常の式に戻していくことができます。
- 「a b ×」「a c ×」「b c ×」を「a×b」「a×c」「b×c」に戻すと「2 （a×b）（a×c）（b×c）＋ ＋ ×」になります。
- 「（a×c）（b×c） ＋」を戻すと「2 （a×b） （a×c＋b×c） ＋ ×」になります。
- 「(a×b) （ac＋bc） ＋」を戻すと「2 (a×b+a×c＋b×c) ×」になります。
- これを戻すと「2×（a×b＋a×c＋b×c）」になります。
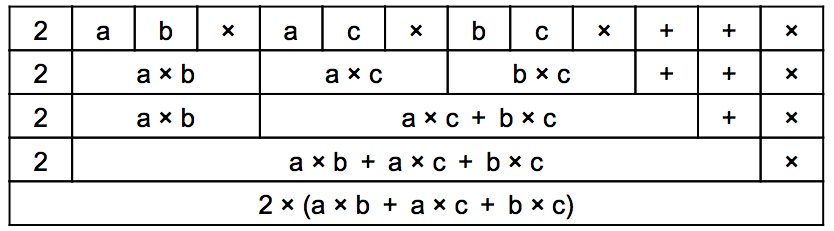
- 正解の式はこのように通常の式に戻していくことができます。
- 解説
- 2つの値を計算するときに，「2＋3」のように命令（計算の記号）を2つの値の真ん中に置く書き方を「中置記法」といいます。
- プログラミング言語の関数呼び出しの「add(2, 3);」のように，命令の後に計算する値を書く書き方を「前置記法」といいます。
- この問題の「2 3 ＋」のように，計算する値の後に命令を書く書き方を「後置記法」といいます。
- 後置記法はForthやPostScriptというプログラミング言語で使われており，PDFの内部でも後置記法が使われています。
- また，「2と3を加える」のように日本語に近い形で読み下すことができることから、ドリトルのような教育用のプログラミング言語でも使われています。
- 出題国: この問題はスロベニアで作成されました。
注があるものを除き, このサイトの内容物は
