SeniorAnswer2019
シニア問題解説(高校2年生・3年生)
- A
2019-ボトルリサイクル-解説
- 考案国:ルーマニア
- 正解
- 説明
- 正解は2です。
選択肢ごとに図を描いてみるとわかりやすいです。図で、白色はwhite、緑色はcolorです。
図1
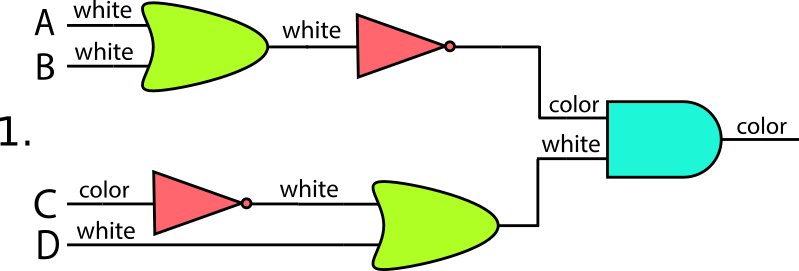
図2
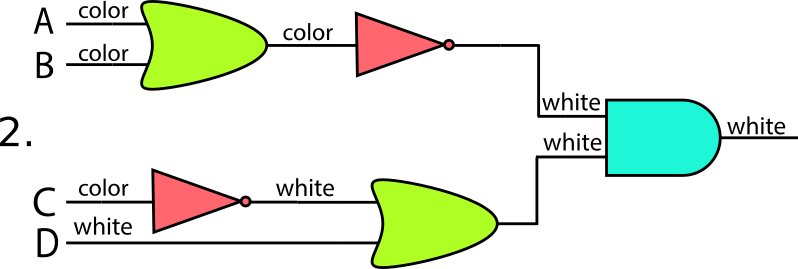
図3
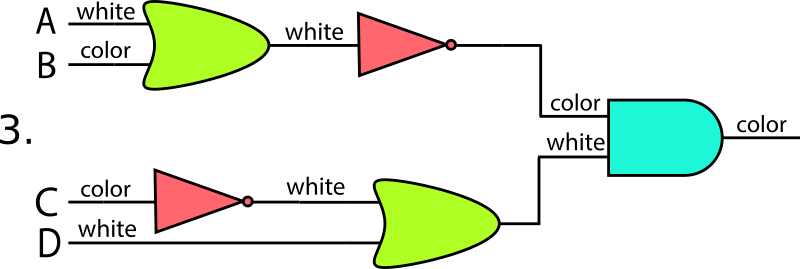
図4
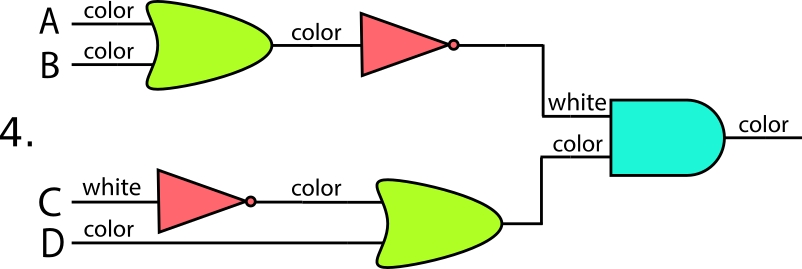
- 正解は2です。
- 白色のボトルを生産するには、次の3種類の入力が考えられます。
A color color color B color color color C color color white D color white white 正解の2
- 実際のコンピュータでは
- コンピュータのCPUは論理回路と呼ばれる微小な電子回路から作られています。論理回路ではNOT, OR, AND, XORなどが使われます。この問題ではAND, OR, NOTを使いました。説明図では実際の電子回路と同じ図で表しています。
- 実際の論理回路では、電気信号の有無で1と0を表します。これは論理回路の真と偽を表しています。この問題では白色(white)を真(1)、緑色(color)を偽(0)の役割で考えました。
- ANDでは両方の入力が真のときに出力が真になります。

- ORでは少なくともどちらかの入力が真のときに出力が真になります。

- NOTでは入力と出力が逆になります。入力が真のときは出力が偽になり、入力が偽のときは出力が真になります。

- ANDでは両方の入力が真のときに出力が真になります。
2019-スカーフ制作機-解説
- 考案国:リトアニア
- 正解
- 説明
- 正解はAです。
図の上の中央にある草は続けて現れることができますが、図の下の中央にある木の枝は繰り返すことができないことに注意しましょう。また、図の出口の青い花から、入口の紫の花に戻ることはできません。
- 正解はAです。
- 実際のコンピュータでは
- この問題のように、入口から矢印をたどりながら「今どこにいて、次はどこに移る」を繰り返して出口に行けるかを表す図をオートマトンまたは状態遷移図と呼びます。
- オートマトンは、プログラムが文法通りに書かれていることを確認したり、PCやスマートフォンで入力された文字を日本語に変換する処理、電卓で数式が正しいことを確認する処理などで利用されています。
- たとえば、多くの電卓では「12+3=」を入力すると正しく計算が行われますが、「12++3=」はエラーになって計算されません。これは電卓の中に「数字の繰り返しと、演算記号と、数字の繰り返しと、最後に=」を表すオートマトンが定義されているため、正しい数式かどうかをチェックできているのです。
2019-トンネル-解説
- 考案国:タイ
- 正解
- 「BBGBGG」または「BBBGGG」
- 説明
- 出口でいちばん左が青(B)になるためには、入口の左がBBであることが必要です。そうでないと出口でいちばん左が緑(G)になってしまいます。
出口でいちばん右が緑(G)になるためには、入口の右がGGであることが必要です。そうでないと出口でいちばん右が青(B)になってしまいます。
そうすると、入力の真ん中の2つはBGかGBになります。どちらの場合も出力の真ん中の2つはBGになるため、両方とも正解であることがわかります。
- 出口でいちばん左が青(B)になるためには、入口の左がBBであることが必要です。そうでないと出口でいちばん左が緑(G)になってしまいます。
- 実際のコンピュータでは
- インターネットの通信で、パケットと呼ばれるデータはIP通信のルールで相手に送られます。ネットワークは「学校内のネットワーク」のように他のネットワークと分かれていて、お互いに直接通信できません。そこでルーターと呼ばれる中継装置を置くことで、適切な経路でパケットを送るようにしています。
2019-倉庫-解説
- 考案国:ロシア
- 正解
- 「10」
- 説明
- 1, 2, 3, 4, 5番のハリネズミと31, 32, 33, 34, 35番のハリネズミは荷物を移動しなくてすみます。
まず、問題の例にあるように、1番のハリネズミは荷物を移動しなくてすみます。実は1番だけでなく、2番から5番のハリネズミも同じです。
次に倉庫の数(5個と6個)を考えると、5で割っても6で割っても余りが0になる数は、0の次は最小公倍数の30です。
そこで、「0に続く1, 2, 3, 4, 5」の次は、「30に続く31, 32, 33, 34, 35」であることがわかります。
- 1, 2, 3, 4, 5番のハリネズミと31, 32, 33, 34, 35番のハリネズミは荷物を移動しなくてすみます。
- 実際のコンピュータでは
- この問題では、データを分割して格納する考え方を扱いました。ハッシュ法と呼ばれるアルゴリズムでは、データを複数の入れ物(倉庫)に分割して格納し、取り出すときは値からどの入れ物に入っているかを計算で求めることで、高速にデータを取り出します。
- わかりやすい例だと、生徒の名簿をアルファベットごとの入れ物に分けておき、「MattiaさんはMの入れ物に入れる」ようなイメージです。
- 今回の問題では、どの入れ物に入っているかを、剰余(割り算の余り)で求めました。例えば倉庫が5個のとき、「1番の倉庫は、1や6のように5で割ったときの余りが1の荷物を入れる」「2番の倉庫は、2や7のように5で割ったときの余りが2の荷物を入れる」「5番の倉庫は、5や10のように5で割ったときの余りが0の荷物を入れる」というやり方です。このようにすると、「13番の荷物はどこにあるかな?」と考えたときに、「13を5で割った余りは3だから3番の倉庫!」とすぐにわかります。
- B
2019-3つの数字で描け-解説
- 考案国:スロバキア
- 正解
- 説明
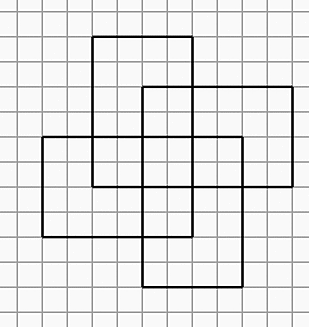
- 実際に、紙に描いてみるとわかりやすいと思います。「1, 4, 1」の場合はこのようになります。
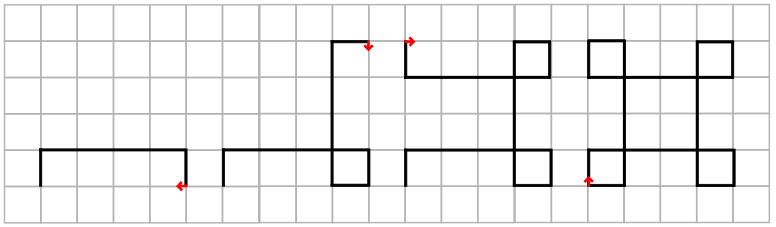
- 実際に、紙に描いてみるとわかりやすいと思います。「1, 4, 1」の場合はこのようになります。
- 実際のコンピュータでは
- コンピュータは与えられたプログラムで動きます。プログラムの命令はひとつひとつが意味を持っていて、コンピュータはそれを順番どおりに実行します。
- この問題では、コンピュータになったつもりで、与えられた命令を実行しました。命令を読んで、ひとつひとつがどのような結果になるかを考えることは、プログラムを作るときと、プログラムを修正するときに重要なスキルです。
2019-赤ずきんちゃんの花壇-解説
- 考案国:ルーマニア
- 正解
- 説明
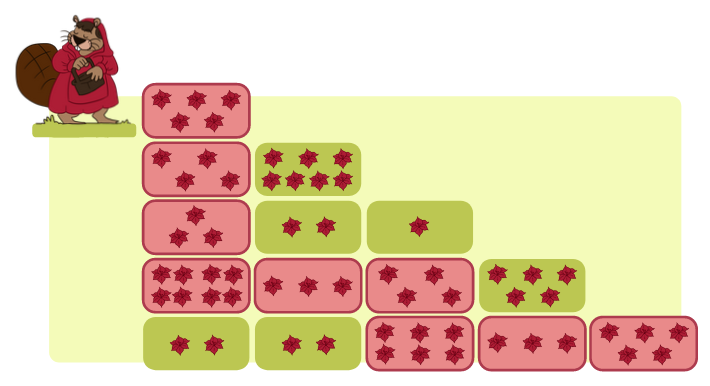
- それぞれの花壇に対して、赤ずきんが左上から集められる花の最大数を求めることができます。計算は次のように行います。
- その花壇がひとつ前の1個の花壇だけから到達できるとき、その花壇の最大値は「その花壇の花の数と、ひとつ前の花壇の最大値の合計」です。
- その花壇がひとつ前の2個の花壇から到達できるとき、その花壇の最大値は「その花壇の花の数と、ひとつ前の花壇の最大値の大きい方の合計」です。
- それぞれの花壇に対して、赤ずきんが左上から集められる花の最大数を求めることができます。計算は次のように行います。
- 実際のコンピュータでは
- この問題では、最適な値を求めるために、動的計画法と呼ばれる戦略を使っています。動的計画法では、複数の中間的な計算結果を記録しておいて利用します。
- 今回の例では、それぞれの花壇に最大値を計算して記録しておくことが相当します。その計算をスタートに近い花壇から徐々に進めていくことで、少しずつ花壇への最大値の計算結果が広がり、やがてゴールの花壇まで到達すると目的の最終結果を得られます。
2019-席順-解説
- 考案国:カナダ
- 正解
- 説明
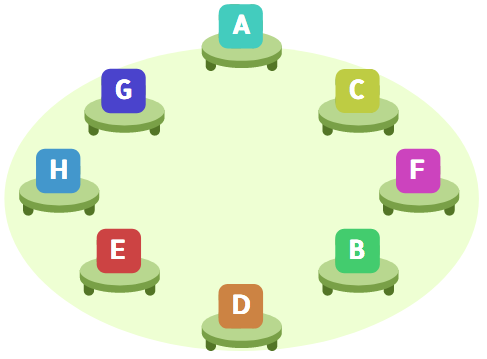
- 条件1から、DはAの向かい側に座ります。AとDの場所が決まりました。
条件5から、EはDの隣に座ります。左右のどちらでも構いません。Eの場所が決まりました。
条件2から、HはEとGの間に座ります。HとGの場所が決まりました。
条件3から、FはAとDの隣ではありません。Fの場所が決まりました。
条件4から、GとCの間には1人が座ります。Cの場所が決まりました。
最後に、空いている場所にBが座ります。これで全員の場所が決まりました。
- 条件1から、DはAの向かい側に座ります。AとDの場所が決まりました。
- 実際のコンピュータでは
- 論理では、規則に従うことと、順序と否定を理解することが重要です。この問題では、「~でない」を意味する否定が重要な役割を果たしていました。たとえば「FはAとDの隣にいない」は「FはAの隣にいないし、FはDの隣にいない」と言うこともできます。
- 論理的な考え方に興味のある生徒は、ドモルガンの法則に興味を持つかもしれません。これは「(AまたはB)ではない」は「(Aでない)かつ(Bでない)」と同じ意味になるという法則です。たとえばある生徒が「(放送部または自転車通学)でない」ということは「(放送部でない)かつ(自転車通学でない)」と同じ意味ということです。
- このように、論理的な表現を記述したり、書き直したり、組み合わせたり、簡潔にしたりするスキルは、コンピュータ科学の世界でとても役に立ちます。
2019-観察-解説
- 考案国:ドイツ
- 正解
- 「BACED」または「EACBD」
- 説明
- 2種類の正解が考えられます。0秒から10秒の間に、誰かが市庁舎のドアを開けるか閉めました。10秒から20秒の間に、TomとTinaが出会いました。彼らは少し離れて立っています。20秒から30秒の間に、TomとTinaは腕を組んで歩きました。並んでいるのでひとつの四角に見えます。30秒から40秒の間に、誰かが市庁舎のドアを開けるか閉めました。40秒から50秒の間に、たくさんの木の葉が散っています。
- 実際のコンピュータでは
- 画像を自動処理することは、空港や駅のような公共の場所で安全を確保するために重要です。権利のない人が侵入したことを確認したり、犯罪の容疑者を特定することが可能です。ただし、プライバシーの問題があるので、継続的に撮影することは注意が必要です。
- この問題では、荒い画像を撮影できる安価なカメラを使って、どのような情報を得られるかを扱いました。実際の画像処理では、スーパーやコンビニのレジでバーコードを読むような簡単な処理から、お客さんの写真からどのような年齢層や性別の人が買物をしているかを判別するような高度な処理までの、さまざまな画像処理が実用化されています。
- C
2019-秘宝の地図-解説
- 考案国:ベトナム
- 正解
- 説明
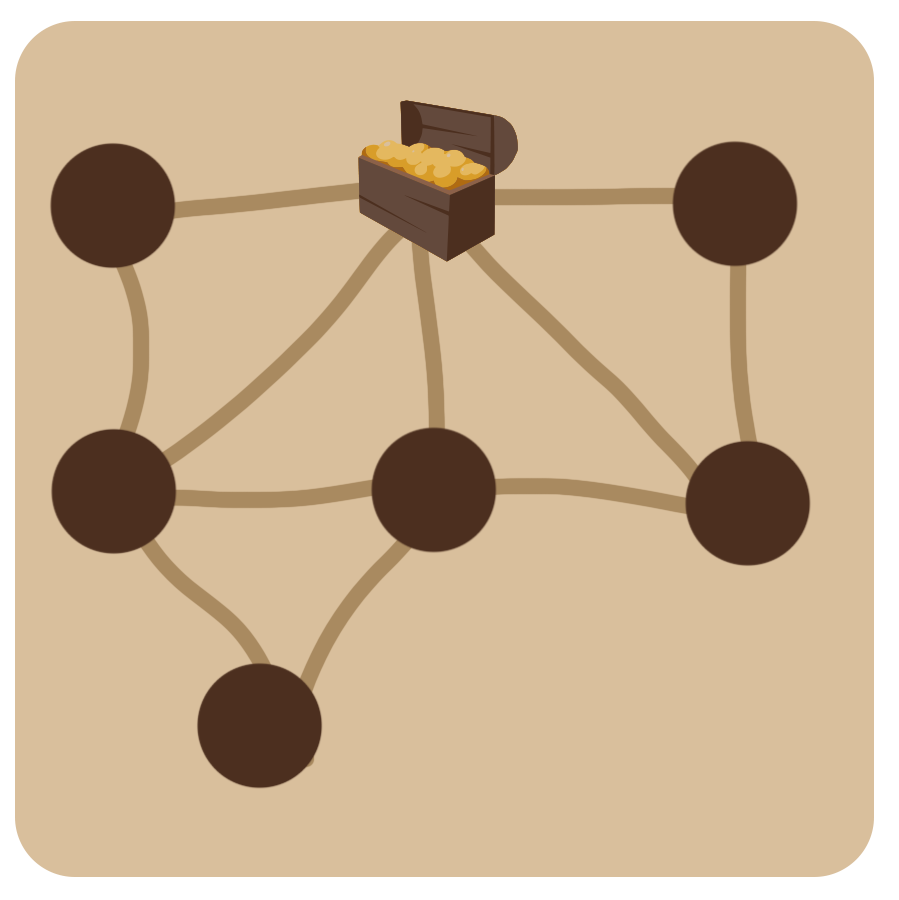
- 地図には7個の区域があります。そこで、宝を含めて丸(●)が6個しかないものは正解ではありません。
- 次に、それぞれの区域が何個の区域と隣り合っているかを数えます。宝のある区域は5個の区域と隣り合っています。そこで、宝から4本しか線が出ていないものは正解ではありません。
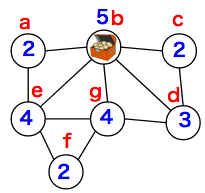
- 残りの2つのどちらが正解かを調べるために、区域にaからgまでの名前を付けて、それらが何個の区域と隣り合っているかを数えてみましょう。
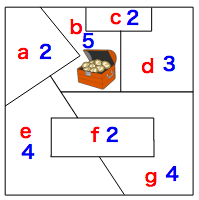
区域aは、b, eの2個と隣接しています。
区域bは、a, c, d, e, gの5個と隣接しています。
区域cは、b, dの2個と隣接しています。
区域dは、b, c, gの3個と隣接しています。
区域eは、a, b, f, gの4個と隣接しています。
区域fは、e, gの2個と隣接しています。
区域gは、b, d, e, fの4個と隣接しています。
隣接している数を見ると、「5個が1区域、4個が2区域、3個が1区域、2個が3区域」あることがわかります。 - 正解でないほうの選択肢を描くと、このようになりました。3個の区域が3個ありますので、正解でないことがわかります。
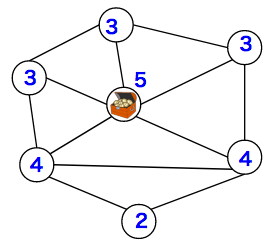
- もうひとつの選択肢を描くとこのようになりました。「5個が1区域、4個が2区域、3個が1区域、2個が3区域」あることがわかります。
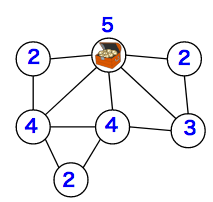
念のために、図に区域を書き込んで確かめることができます。
- 実際のコンピュータでは
- この問題では、点(頂点)と線(辺)で表される「グラフ構造」が実際の問題を解くときに有効なことを学びました。頂点は区域を表し、辺は「区域が隣り合っている」という関係を表しています。
- グラフ構造は、複数のものごとの関係を表すときに便利です。数学者とコンピュータ科学者は、グラフ構造を使うことで、現実の問題を解決するためのたくさんの有用なアルゴリズムを考えてきました。
2019-ビーバー宅配便-解説
- 考案国:カナダ
- 正解
- 「25」
- 説明
- Aからスタートして、同じ道を通らずにすべての街を通る移動ルートは以下の4種類しかありません。
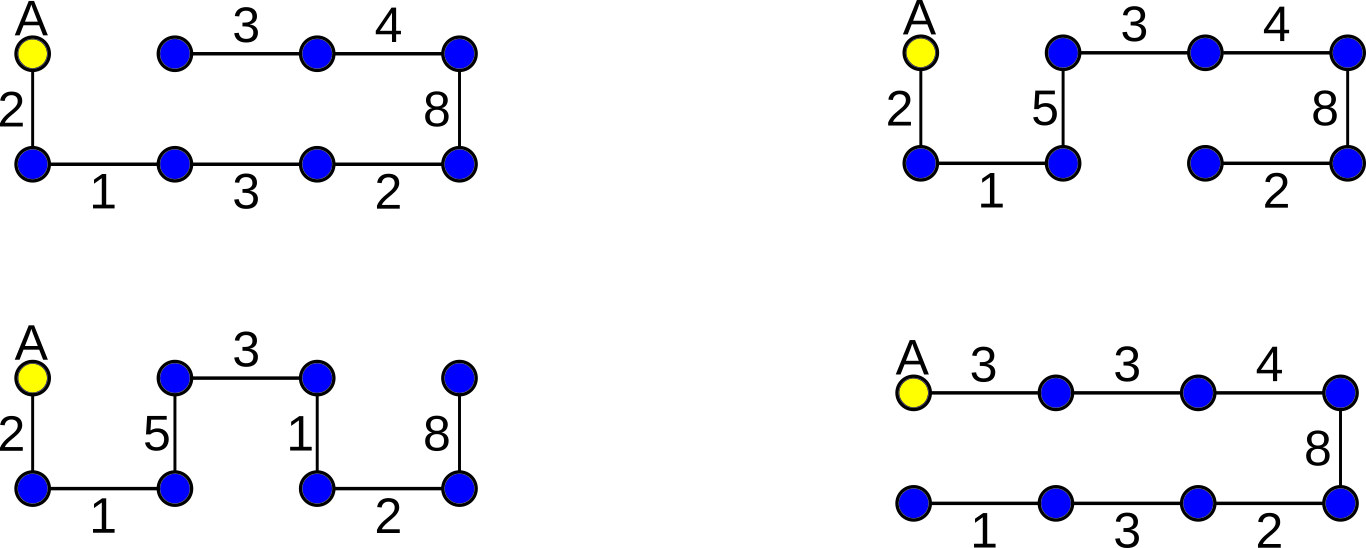
それぞれの移動ルートで得られる賃金です。2+1+3+2+8+4+3 = 23 2+1+5+3+4+8+2 = 25 2+1+5+3+1+2+8 = 22 3+3+4+8+2+3+1 = 24
計算結果を見ると、これらの賃金の最大値は25であることがわかります。
- Aからスタートして、同じ道を通らずにすべての街を通る移動ルートは以下の4種類しかありません。
- 実際のコンピュータでは
- コンピュータ科学では、このような図は「グラフ」と呼ばれます。街に相当する点は「頂点」、道に相当する線は「辺」です。
- グラフの最適な経路を探索するために複数のアルゴリズムが使われます。すべての頂点を1回だけ通る経路はハミルトン路です。今回の問題ではハミルトン路であることに加え、収益が最も高くなる経路を探索しました。
2019-回って回って回って-解説
- 考案国:ロシア
- 正解
- 「短い,長い,長い,短い」
- 説明
- 「短い,長い,長い,短い」だけが、どの向きで始めても、最後の回転で同じ向きになります。
- 実際のコンピュータでは
- この問題は、以下の図に示す有限状態オートマトンを扱っています。
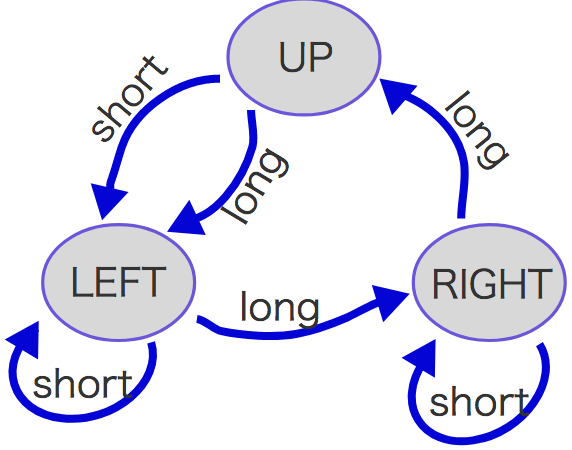
状態は円で表され、三角形の軸から遠い頂点が上向き(UP)、左向き(LEFT)、右向き(RIGHT)の3つの状態があります。遷移は矢印で表され、それぞれの状態から、出っ張りが短い(short)、長い(long)の2つの遷移が他の状態または自分自身の状態に向いています。
- この問題は、以下の図に示す有限状態オートマトンを扱っています。
2019-○△□-解説
- 考案国:ウクライナ
- 正解
- 「4, 3, 2, 3, 2, 1, 1, 5, 1」
- 説明
- 複数の解き方が考えられます。ひとつの正解例を説明します。
- ルールをよく見ると、奇数個の円(●)を作る命令はないことがわかります。そこで、6個の円(●)を作り、ボタン5で3個を消すことを考えましょう。6個の円(●)を作るには、3個の三角(▲)があればボタン1で作れます。このようにして、「3個の三角(▲)を作る」という中間目標ができました。これは「4, 3, 2, 3, 2」の順にボタンを押すことで作ることが可能です。
1) (ボタン4)
2) (ボタン3)
3) (ボタン2)
4) (ボタン3)
5) (ボタン2)
6) (ボタン1)
7) (ボタン1)
8) (ボタン5)
9) (ボタン1)
- 実際のコンピュータでは
- この問題では、ボタンは形式言語の規則を表していました。形式言語では、初期の語(この問題では2つの四角(■■))を規則によって別の語に置き換えていくことができます。
- コンピュータの世界では、プログラミング言語は形式言語で、この問題のような構文規則で定義されています。そして、「ifは分岐を表す」のような構文の意味も定義されます。
(シニア問題に戻る)

 注があるものを除き, このサイトの内容物は
注があるものを除き, このサイトの内容物は