BenjaminAnswer2011

ベンジャミン問題解説(小学５年生・６年生)

A
「三原色」解答
- 正解は
  - 最下行を見ると、青と緑の繰り返しになっている。また、右端の列を見ると、緑と赤の繰り返しになっている。
- 解説
  - パソコンや携帯電話の画面では、「赤、緑、青」の三色を組み合わせることで、さまざまな色を表現しています。
  - 元の絵
  - 拡大図
「カエルのジャンプ」解答
- 正解は「０，０，０，６，６，６，４，４，２，２，４，４，１」
  - カエルは最初に右に3回ジャンプする。右方向は0なので、並びは「０，０，０」で始まる。
- 解説
  - コンピュータでは、「０，６」のような命令の並びで、動作を制御しています。
  - このような命令の並びをプログラムと呼んでいます。
「謎のメッセージ」解答
- 正解は「たのしいね」
  - 50音をそれぞれ3文字後ろにずらして暗号化しているので，3文字前にずらせば解読（復号）できる。
  - て→た
  - ふ→の
  - そ→し
  - お→い
  - ひ→ね
- 解説
  - 文字を決まった数だけ隣の文字と置き換える暗号です。
  - 古代ローマのカエサルにちなんでシーザー暗号と呼ばれています。
B
「都市」解答
- 正解は「63651」
  - 人口の多い順なので、最後から2番目のビバリアはグラフの上から2番目になる。
- 解説
  - ある規則で並んだデータの対応を読み取る問題です。
「白黒画像」解答
- 正解は「H」
  - 左から「白の数」「黒の数」「白の数」「黒の数」の順に並んでいる。
    黒白白白黒
    黒白白白黒
    黒黒黒黒黒
    黒白白白黒
    黒白白白黒
- 解説
  - 同じ値の並ぶ数でデータを表現する方法で、ランレングス符号と呼ばれます。
  - 白い紙に文字を印刷した場合は、白の点が続く部分が多いため、少ないデータで画像を表現することができます。そのため、ファクシミリ（FAX）の送受信などで利用されています。
「ピザの配達」解答
- 正解は「4を出している家」
  - 看板は8,4,2,1という2進数の値になっている。
  - 11を表す組み合わせは「8,2,1」のみ。
- 解説
  - ある数を表す2進数の各桁の組み合わせは1通りです。
  - 11を2進数で表すと「1011」となり、4の位だけが0になります。
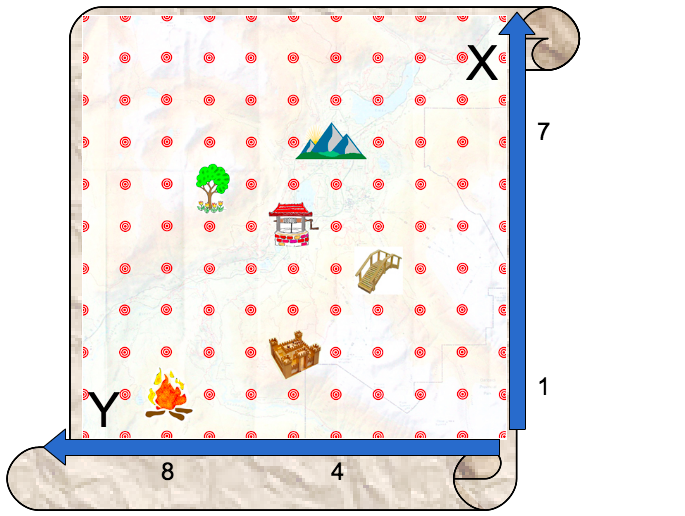
「宝探しの地図」解答
- 正解は「岩のところにある」
  - たき火の場所を見ると、（1|8）は地図の右下からの位置であることがわかる。
  - （X|Y）と考えると、縦がXで、横がYになる。
  - 宝物は（7|4）の場所にある。地図で見ると岩の場所である。
- 解説
  - 画面上の点の位置は、「左端からxドット、上端からyドット」のように、画面の端からの縦横の座標で表現することができます。
C
「ビボナッチ」解答
- 正解は「6」
  - ビーバーは、自分より前の2人の数を足した数を答えていく。
  - ひとりずつ当てはめていくと、6番目で13になり、10より大きい数になる。
    番目言う数
    1 1
    2 2
    3 3
    4 5
    5 8
    6 13
- 解説
  - このような数の並びはフィボナッチ数列と呼ばれます。
「飛行機格納庫」解答
- 正解は「4」
  - 大型機を4機入れる配置は、大きく3通りあります。
    - 大型機を「左の格納庫に縦に1機」「真ん中の格納庫に横に2機」「右の格納庫に横に1機」置いたときは、小型機は「左の格納庫に3機」「右の格納庫に1機」の計4機置けます。
    - 大型機を「左の格納庫に横に2機」「真ん中の格納庫に横に2機」「右の格納庫に0機」置いたときは、小型機は「右の格納庫に3機」の計3機置けます。
    - 大型機を「左の格納庫に横に2機」「真ん中の格納庫に横に1機」「右の格納庫に横に1機」置いたときは、小型機は「真ん中の格納庫に2機」「右の格納庫に1機」の計3機置けます。
  - よって，小型機は「左の格納庫に3機」，「真ん中の格納庫に0機」、「右の格納庫に1機」の計4機を配置することが最大になります。
- 解説
  - ある領域に、できるだけ無駄のないように配置する問題で、詰め込み問題と呼ばれます。
  - CPUなどVLSIの設計時に、どのようにモジュールを配置するかなどの検討に用いられています。
「丸太運び」解答
- 正解は「大きい丸太1本と中くらいの丸太2本」
  - 丸太とコインの関係を考えると、次のようになる。できるだけ、大きな丸太と中くらいの丸太を入れるのがよさそう。
    - 大きな丸太は1kgあたりコイン1.67枚。
    - 中くらいの丸太は1kgあたりコイン1.5枚。
    - 小さな丸太は1kgあたりコイン0.5枚。
  - 7kgのリュックサックに入れる組み合わせとして、大きな丸太を0本、1本、2本の場合を考えてみる。
    - 大きな丸太0本＋中くらいの丸太3本＋小さな丸太1本＝コイン9.5枚
    - 大きな丸太1本＋中くらいの丸太2本＋小さな丸太0本＝コイン11枚
    - 大きな丸太2本＋中くらいの丸太0本＋小さな丸太1本＝コイン10.5枚
- 解説
  - 入れられる量の決まったリュックサックに、どのような組み合わせで入れると最も効率がよいかという問題で、ナップザック問題と呼ばれます。