カデット問題/A水力発電
水力発電
ビーバーは木のパイプでHの発電所に水を送る仕組みを作りました。水はAからGの場所から入ります。パイプが合流するつなぎめは二種類あります。
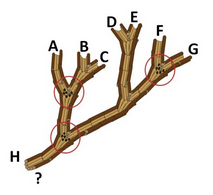
赤い丸で囲まれたつなぎめでは、両方のパイプに水が来たときだけ水が流れます。
赤い丸で囲まれていないつなぎめでは、どちらかから水が来れば水が流れます。
どの状態のときにHに水が流れるでしょう？
- 解説を見る
- 正解は「A, C, Dに水が来て、B, E, F, Gに水が来ない」
赤い丸で囲まれたつなぎめを見て、両方から水が来ているかを考えればよい。- 「A, B, C, Fに水が来て、D, E, Gに水が来ない」では、Gに水が来ないので G と F の合流で水が流れず、水は H まで流れない。
- 「A, B, Gに水が来て、C, D, E, Fに水が来ない」では、Fに水が来ないので G と F の合流で水が流れず、水は H まで流れない。
- 「B, C, E, Gに水が来て、A, D, Fに水が来ない」では、Fに水が来ないので G と F の合流で水が流れず、水は H まで流れない。また、A に水が来ていないので A と B,C からの合流で水が流れず，このことからも水がHまで流れないことが分かる。
- 解説
論理演算に関する問題です。「真」（この問題では、「水が流れる/来る」の相当）と「偽」（この問題では、「水が流れない/来ない」に相当）の２種類の値を「かつ (∧)」と「または (∨)」を組合せて考えます。「P ∧ Q」は P と Q の両方が「真」のとき「真」となり、そうでないときは「偽」になります。「P ∨ Q」は P か Q の少なくとも１つが「真」のとき「真」となり、そうでないときは「偽」となります。
この問題の図の状況は、次のように表すことができます。(A ∧ (B ∨ C)) ∧ (D ∨ E) ∨ (F ∧ G))
図の状況で水が流れるのは、この式が「真」となるように A, B, C, D, E, F, G に「真」・「偽」を割り当てた場合です。
- 正解は「A, C, Dに水が来て、B, E, F, Gに水が来ない」
注があるものを除き, このサイトの内容物は
